Погрешность и сходимость интерполяции

Интерполяция полиномом (п+1) степени имеет одну особенность. Полином всегда описывает какой-то колебательный процесс на отрезке интерполяции, но за его пределами его график резко уходит от интерполируемой функции. Характер изменения функции относительно можно изобразить графически, например, при пяти узловых точках (рисунок 18, функция условно представлена прямой линией). Следовательно, функция здесь – многочлен пятой степени. Амплитуда периодической функции имеет переменную величину – в центре интервала она всегда меньше, чем на периферии. Тогда можно говорить о наличии функции 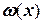, описывающей изменение амплитуды первичной функции, т.е. огибающей по вершинам полуволн функции . Текущее значение амплитуды отклонения функции

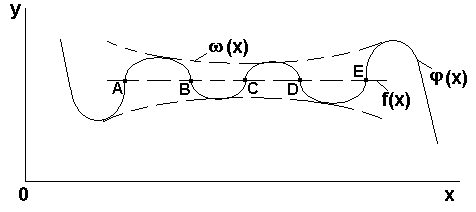
Рисунок 18 - Графическая интерпретация ошибки интерполирования

от функции - это текущее значение погрешности приближения. Очевидно, что эта погрешность может быть записана как функция:

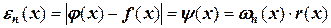
Погрешность интерполирования не является постоянной величиной. Она всегда минимальна в центре интервала интерполяции и возрастает к границам. Вне отрезка интерполяции функция резко отдаляется от функции . Конечная формула для расчета ошибки интерполяции имеет вид:

.

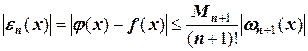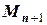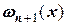Такая формула требует знания и . Но 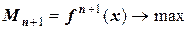, т.е. это максимальное значение функции на всем отрезке интерполирования. Вычисление функции 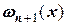достаточно трудоемкая процедура. Но, если отрезки интерполирования равновелики, то формула расчета погрешности упрощается, принимая вид:

.

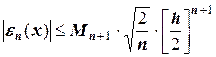Отсюда следуют некоторые выводы. Для того чтобы повысить точность интерполирования, можно (порознь или одновременно) стремиться к следующему: снижать длину участков интерполирования или (и) повышать количество узловых точек. Наиболее эффективно снижение длины участков. Увеличение узловых точек не всегда дает положительный результат, так как для каждой функции существует критическое значение участков интерполирования.