Постановка задачи об аппроксимации функций

В практике вычислений зачастую возникают задачи, которые требуют привлечения методов приближения функции. В основном их можно свести к двум задачам:

- замена некоторой функции, заданной аналитически или таблично, другой функцией, близкой к исходной, но более простой и удобной для вычислений (например, в “неберущихся“ интегралах

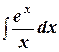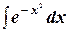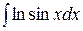; ; и т.п.

подынтегральная функция может быть заменена другой, более простой);

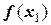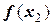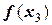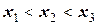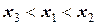- когда имеются значения функции и , но надо вычислить , где или или .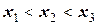

В основе решения таких задач лежит подмена одной функции другой функцией . Такая подмена называется аппроксимацией или приближением функции функцией . При реализации этого процесса неизбежно надо получить ответы на следующие вопросы.

1) Что известно о функции ? Задана ли она аналитически или таблично, какова степень ее гладкости и доступны ли ее производные? Как расположены точки в интересующей части области определения функции, где известны ее значения?

2) Какому классу (семейству) функций должна принадлежать функция ?

3) Что понимать под “близостью“ между и ? Иначе, какой принять критерий согласия между ними?

Итак, задача аппроксимации функции состоит в построении для исходной функции такой функции , что 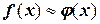, причем левая часть этого приближенного равенства должна быть обусловлена ответами на вопросы первой группы, правая часть – второй группы, а ответ на третий вопрос должен уточнить значение связывающего и символа “ ≈ “.

Для аппроксимации широко используются следующие классы функций: многочлены, тригонометрические функции, показательные функции. Особенно часто используются многочлены, так как они очень легко дифференцируются и интегрируются. В качестве критерия близости исходной и приближающей функций можно выбрать:

а) точное совпадение приближаемой и приближающей функции в так называемых узловых точках (интерполяция);

б) усредненное положение приближающей функции по отношению заданных значений приближаемой функции (выдвигаются конкретные критерии близости, например, минимизация суммы квадратов отклонений одной функции от другой).