Основные положения. Необходимость решать системы линейных уравнений возникает достаточно часто как в теоретических приложениях

Необходимость решать системы линейных уравнений возникает достаточно часто как в теоретических приложениях, так и при решении большого круга практических задач. Система линейных уравнений имеет вид:

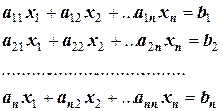. (7)

В математическом анализе показано, что она может быть записана в матричном виде. Коэффициенты при неизвестных образуют квадратную матрицу А, которая носит название определителя системы, а свободные члены правой части уравнений записываются в виде вектора-столбца В:

; ;

.

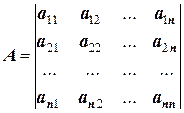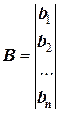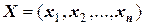Тогда в векторной форме система записывается:

.

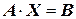В принципе известны формулы Крамера, позволяющие получить точное решение:

,

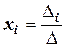где 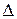- определитель системы (),

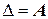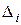- определитель матрицы, которая получается из матрицы А заменой столбца с номером (i ) столбцом свободных членов В.

Однако в качестве универсального метода решения системы данные формулы совершенно неприменимы, так как при подсчете каждого определителя по приведенной выше формуле надо вычислять ( n! ) слагаемых, что нереально даже при весьма умеренных n. Например, при n=3 по правилу Серрюса получаем:

,

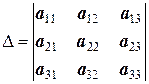или

.

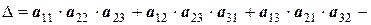
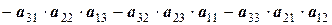Мы имеем шесть пар произведений, т.е. при матрице размерностью (n∙ п), надо выполнить по крайней мере 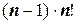действий. Если, например, принять n=100 (а бывают системы и больше), то будем иметь 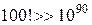. Если одно вычисление выполнять за 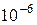с. (что для современных машин вполне реально), время расчета только одного определителя составит 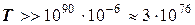лет. Фактически же в настоящее время решаются системы гораздо более высокого порядка(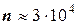). Для этого применяют другие методы. Их множество. В целом они разделяются на две группы: прямые и итерационные.

Прямые методы позволяют теоретически получить точное решение задачи за конечное число арифметических операций. В реальности точное решение получить нельзя, т.к. при арифметических вычислениях неизбежны приближенные методы расчета с какой-то ошибкой.

Итерационные методы (или методы последовательных приближений) позволяют вычислять последовательность векторов переменных (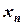), сходящуюся при .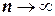