Сущность метода простой итерации

Этот метод является одним из наиболее удобных и эффективных. Как видно из его названия, корнень уточняется с использованием итерационной последовательности.

Мы уже знакомы с приемом отделения корня уравнения, когда функция f(x) преобразовывается в виде разности двух функций 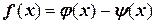и затем корень отделяется из условия 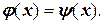В методе простых итераций используют тот же прием, однако одна из приведенных функций всегда определена, а именно 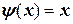. Тогда любая функция f(x) каким-либо способом (см. ниже) преобразуется к виду 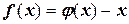и если 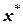- корень уравнения , то 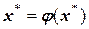. Из этой предпосылки следует, что итерационный процесс должен быть организован так, чтобы достигалось соотношение 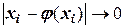. Метод реализуется следующим образом.

Геометрически на интервале отделения корня уравнение представляется в виде двух пересекающихся линий и 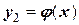, рисунок 14. Тогда абсцисса точки М(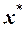) является корнем уравнения f(x).

Полагая, что известно начальное приближение корня x₀, построим итерационный процесс на основе рекуррентной формулы 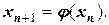Назначим x=x₀. Для него точка А имеет ординату 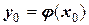. Перемещаясь теперь вправо до линии y₁=x,

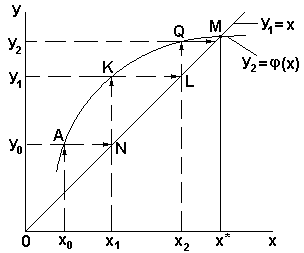
Рисунок 14 - Алгоритм метода простых итераций

получим точку N, координаты которой будут (x₁; φ (x₀) ). Очевидно равенство двух отрезков - 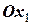и 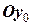, т.е. реализована запись реккурентной формулы 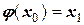. Повторяя алгоритм, найдем значение φ (x₁), т.е. определим точку К (x₁; φ (x₁) ). Перемещаясь опять из точки К вправо до линии y₁=x, получим точку L с координатами ( x₂; φ (x₁) ). Далее, при x=x₂ получим точку Q( x₂; φ (x₂) ).

В конечном итоге итерационный ряд x₀; x₁; x₂…x_n в пределе при 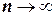достигнет точного значения корня. Естественно, процесс итерации следует остановить тогда, когда будет достигнуто неравенство 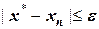. На практике 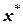является неизвестной величиной. Поэтому в методе простых итераций принимают два подхода к оценке точности результатов расчета:

- приближенная оценка: ;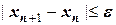

- предпочтительная оценка: ,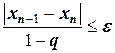

где .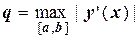

Метод простых итераций является более общим методом решения нелинейных уравнений, чем ранее рассмотренные. Прежде всего это относится к методу Ньютона. Он имеет ряд особенностей, которые мы рассмотрим ниже.