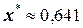Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Условие сходимости метода
|
|
Эта проблема наиболее наглядно может быть рассмотрена на основе геометрической интерпретации метода. Схематично он представлен на рисунке 15.
Рассмотрим процесс итерации, представив упрощенно функцию  в виде прямой линии, соответствующим образом расположенной относительно линии y1=x. Предположим, что значение корня соответствует абсциссе точки М. Проведем через эту точку, лежащую на прямой
в виде прямой линии, соответствующим образом расположенной относительно линии y1=x. Предположим, что значение корня соответствует абсциссе точки М. Проведем через эту точку, лежащую на прямой 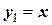 , дополнительную линию ( n-n ) под углом
, дополнительную линию ( n-n ) под углом 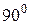 , тем самым разделим все координатное поле на четыре квадранта I; II; III; IV. Возможны четыре типа взаимного расположения линий двух исходных функций.
, тем самым разделим все координатное поле на четыре квадранта I; II; III; IV. Возможны четыре типа взаимного расположения линий двух исходных функций.
Проведем через точку M прямые  двухвариантно так, чтобы обе прямые прошли через II и IV квадранты. Важной характеристикой этих прямых будет угол наклона к оси ox. Очевидно, что на рисунке 15 a этот угол
двухвариантно так, чтобы обе прямые прошли через II и IV квадранты. Важной характеристикой этих прямых будет угол наклона к оси ox. Очевидно, что на рисунке 15 a этот угол  , а соответственно
, а соответственно 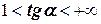 . На рисунке 15б соответственно
. На рисунке 15б соответственно 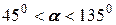 и для него
и для него 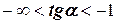 . Если назначить в виде первого приближения какое-то значение
. Если назначить в виде первого приближения какое-то значение 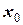 и начать итерационный процесс, то становится очевидно, что на рисунке 15 а он расходится односторонне, а на рисунке 15 б он также расходится но циклически (двусторонне). Главное, что он расходится.
и начать итерационный процесс, то становится очевидно, что на рисунке 15 а он расходится односторонне, а на рисунке 15 б он также расходится но циклически (двусторонне). Главное, что он расходится.
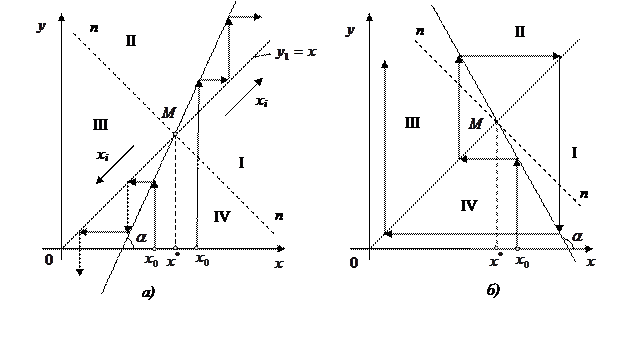

Рисунок 15 - К обоснованию сходимости метода простых итераций
Выполним очередное построение. Проведем линии  через точку М так, чтобы они проходили в I и III квадрантах. На рис.15 в угол
через точку М так, чтобы они проходили в I и III квадрантах. На рис.15 в угол 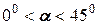 и соответственно
и соответственно 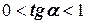 , а на рис.15 г угол
, а на рис.15 г угол 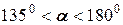 и его тангенс изменяется в пределах
и его тангенс изменяется в пределах 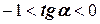 . Если принять за первое приближение какое-то значение
. Если принять за первое приближение какое-то значение 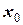 и организовать итерационный процесс, то становится очевидно, что он сходится, причем на рис.15 в он сходится односторонне, а на рис.15 г наблюдается двусторонняя сходимость.
и организовать итерационный процесс, то становится очевидно, что он сходится, причем на рис.15 в он сходится односторонне, а на рис.15 г наблюдается двусторонняя сходимость.
Обобщим результаты построений:
- процесс простой итерации сходится, если соблюдается условие 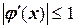 ;
;
- если 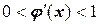 , то итерационный процесс сходится односторонне,
, то итерационный процесс сходится односторонне,
а если 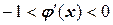 , то он сходится двусторонне;
, то он сходится двусторонне;
- если 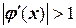 , то процесс простой итерации расходится.
, то процесс простой итерации расходится.
Видим, что применение метода простой итерации имеет свою специфику по области применения, что, однако, как будет показано ниже, не является непреодолимым препятствием для его применения.
3.8.3 Особенности преобразования первичной функции
Выше было показано, что метод простой итерации требует обязательного выполнения условия 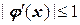 . Действительно, вид функции
. Действительно, вид функции 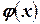 , как результат преобразования первичной функции f(x) к виду
, как результат преобразования первичной функции f(x) к виду 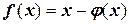 возможен несколькими способами. Отсюда следует, что функция
возможен несколькими способами. Отсюда следует, что функция 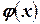 не может быть наперед задана. Поэтому для того, чтобы к функции f(x) возможно было применение метода простой итерации, следует иметь такой вид
не может быть наперед задана. Поэтому для того, чтобы к функции f(x) возможно было применение метода простой итерации, следует иметь такой вид 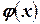 , чтобы выполнялось условие
, чтобы выполнялось условие 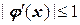 .
.
Рассмотрим классический пример вычисления квадратного корня. Для того, чтобы вычислить корень квадратный из числа а, нужно численным методом решить уравнение 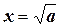 . Это приводит к другому уравнению
. Это приводит к другому уравнению 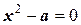 , (
, (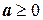 ). Преобразуем его к виду y=y(x). Это можно сделать, например, тремя следующими способами.
). Преобразуем его к виду y=y(x). Это можно сделать, например, тремя следующими способами.
Способ 1. Разделив исходное уравнение на x, получим:
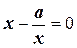 или
или 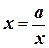 .
.
Тогда 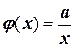 . (5)
. (5)
Проверим условие сходимости метода. Очевидно, что
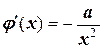 .
.
Рассматривая итерационный процесс как предельный переход, можно записать:
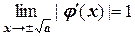 ,
,
но всегда 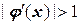 .
.
Поэтому, если на основании функции (5) осуществим итерационный процесс, то он будет расходиться.
Способ 2. К левой и правой частям уравнения 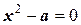 прибавим x. Получим:
прибавим x. Получим:
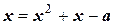 .
.
Тогда 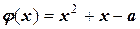 ,
,
а соответственно 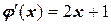 .
.
Так как 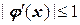 по условию, то
по условию, то  при
при 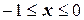 и
и 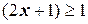 при
при 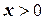 и
и 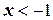 . Следовательно, если принять
. Следовательно, если принять 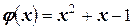 , то применение этой функции будет ограничено только участком [ -1< x< 0 ].
, то применение этой функции будет ограничено только участком [ -1< x< 0 ].
Способ 3. Выполним следующие преобразования:
 ;
; 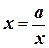 ;
;
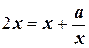 ;
; 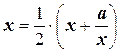 .
.
В результате получили еще одну функцию
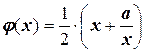 .
.
Найдем ее производную:
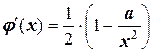 .
.
Если 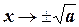 , то
, то 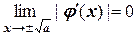 .
.
В таком случае процесс итерации должен очень быстро сходиться. Действительно, это уравнение используется в компьютерах для вычисления квадратного корня. Таким образом, в методе простой итерации важен выбор вида функции 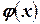 .
.
Задача 10. Вычислить 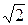 с точностью до пяти верных цифр после запятой. Функцию
с точностью до пяти верных цифр после запятой. Функцию 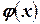 принять равной:
принять равной:
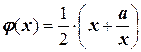 .
.
Решение. Вычисления будем проводить по рекуррентной формуле:
 .
.
Выполним два расчета, приняв сначала  , затем
, затем  . Определим скорость сходимости. Составим расчетные таблицы, незначительно видоизменив рекуррентную формулу.
. Определим скорость сходимости. Составим расчетные таблицы, незначительно видоизменив рекуррентную формулу.
Таблица 7 - Вычисление 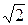 при условии
при условии 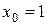
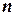
| 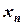
| 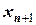
| 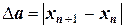
| 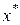
|
| 1, 5 | 0, 5 | 1, 0 | ||
| 1, 5 | 1, 41666 | 0, 0833 | 1, 0 | |
| 1, 41666 | 1, 414215 | 0, 00245 | 1, 41 | |
| 1, 4142 | 1, 4142135 | 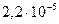
| 1, 414213 |
Таблица 8 - Вычисление 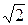 при условии
при условии 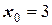
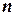
| 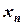
| 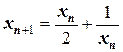
| 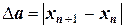
| 
|
| 1, 8333 | 1, 1666 | - | ||
| 1, 8333 | 1, 46212 | 0, 3712 | 1, 0 | |
| 1, 46212 | 1, 41499 | 0, 04712 | 1, 4 | |
| 1, 4142138 | 1, 4142135 | 7, 866∙ 10-4 | 1, 414 | |
| 1, 4142138 | 1, 4142135 | 3∙ 10-7 | 1, 414213 |
Вычисления дают следующий ответ: 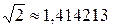 .
.
Задача 11. Отделить корни и найти методом простой итерации корень с точностью до 0, 001 уравнения 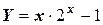 .
.
Решение. Запишем это уравнение в следующем виде (положив Y=0):
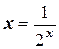 ,
,
тогда 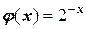 .
.
Найдем производную 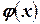 :
:
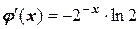
и запишем условие сходимости:
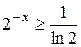 .
.
Выполним ряд преобразований и получим предельное значение х:
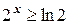 ;
;
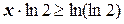 ;
;
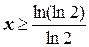 ;
;
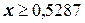 .
.
Попробуем отделить корень, выполнив небольшой расчет (см. таблицу 9).
Таблица 9 - Отделение корня уравнения
| x | 0, 5 | |||
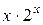
| 0, 707 | |||
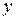
| -1 | -0, 293 |
Видим, что на отрезке [0, 5; 1] происходит изменение знака функции. Следовательно, на этом участке может находиться корень нашего уравнения. Рассчитаем значение 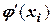 на границах интервала:
на границах интервала:
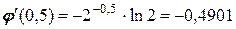 ;
; 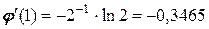 .
.
Так как на исследуемом участке 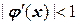 , метод итерации будет сходиться. Составим расчетную таблицу, приняв
, метод итерации будет сходиться. Составим расчетную таблицу, приняв  .
.
Таблица 10 - Расчетная таблица к уравнению 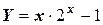
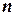
| 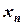
| 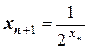
| 
|
| 0, 5 | 0, 5 | ||
| 0, 5 | 0, 7071 | 0, 2071 | |
| 0, 7071 | 0, 61254 | 0, 09455 | |
| 0, 61254 | 0, 65404 | 0, 04150 | |
| 0, 65404 | 0, 63549 | 0, 01854 | |
| 0, 63549 | 0, 643718 | 0, 00822 | |
| 0, 643718 | 0, 64006 | 0, 003656 | |
| 0, 64006 | 0, 641686 | 0, 001626 | |
| 0, 641686 | 0, 64096 | 0, 000722 |
Следовательно, корень искомого уравнения равен