
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Полиномиальная интерполяция
|
|
Пусть на отрезке задано дискретное множество несовпадающих точек 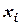 , которые называются узлами, в которых известны значения функции
, которые называются узлами, в которых известны значения функции  . Иначе, функция
. Иначе, функция  задана таблично:
задана таблично:
Таблица 17 – Табличная запись исходной функции
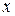
| 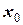
| 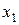
| 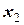
| …. | 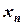
|

| 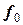
| 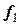
| 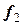
| …. | 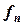
|
Интерполяцией называется процесс приближения функции  функцией
функцией  при условии, что в узлах сохраняется строгое равенство
при условии, что в узлах сохраняется строгое равенство
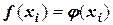 ,
, 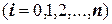 .
.
Иногда этот процесс называют Лагранжевой интерполяцией. Очевидно, что график функции  должен проходить так, что по крайней мере в (п+1 ) заданных точках он пересечет или коснется графика функции
должен проходить так, что по крайней мере в (п+1 ) заданных точках он пересечет или коснется графика функции  , рисунок 16.
, рисунок 16.
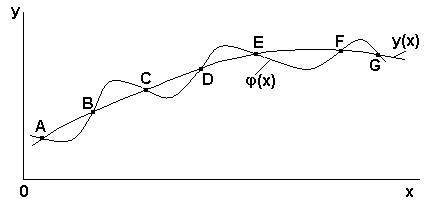
Рисунок 16 - Принцип интерполяции функции
Легко представить, что таких графиков  , проходящих через заданные точки, можно изобразить сколько угодно, и они могут отличаться от графика
, проходящих через заданные точки, можно изобразить сколько угодно, и они могут отличаться от графика  сколь угодно сильно, если не накладывать на эти функции определенных ограничений.
сколь угодно сильно, если не накладывать на эти функции определенных ограничений.
Рассмотрим процедуры приближения функции  многочленом степени (п). Тогда задача интерполяции (полиномиальной) формулируется так: для функции
многочленом степени (п). Тогда задача интерполяции (полиномиальной) формулируется так: для функции  , заданной таблицей, найти многочлен
, заданной таблицей, найти многочлен  такой, чтобы выполнялась совокупность условий интерполяции
такой, чтобы выполнялась совокупность условий интерполяции 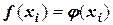 ,
, 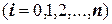 . Найти многочлен
. Найти многочлен  - это значит, учитывая его каноническую форму
- это значит, учитывая его каноническую форму
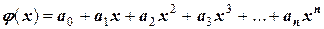 ,
,
найти все его коэффициенты 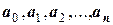 . Для этого есть как раз (п+1) условие (табличная функция
. Для этого есть как раз (п+1) условие (табличная функция  ). Таким образом, чтобы многочлен
). Таким образом, чтобы многочлен  был интерполяционным для функции
был интерполяционным для функции  , нужно, чтобы его коэффициенты удовлетворяли системе уравнений:
, нужно, чтобы его коэффициенты удовлетворяли системе уравнений:

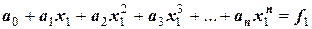
………………………………………..
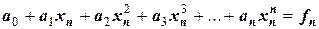 .
.
Заметим, что неизвестными в этом случае являются коэффициенты 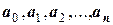 , а известными являются значения
, а известными являются значения 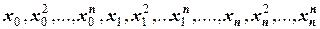 . Можно вышеприведенную систему уравнений представить и в векторной форме:
. Можно вышеприведенную систему уравнений представить и в векторной форме:
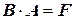 ,
,
где 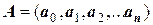
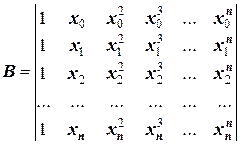 ;
; 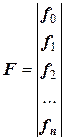
Определитель В в курсе алгебры называется определителем Вандермонда. Если он равен нулю, то существует единственное решение системы. Таким образом, процедура интерполяции сводится к решению системы линейных уравнений.
Задача 16. Проинтерполировать функцию, заданную таблично, найдя коэффициенты многочлена степени п=3 решением линейных уравнений.
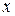
| 0, 5 | 1, 0 | 1, 5 | 2, 0 |
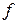
| 2, 75 | 4, 0 | 8, 75 | 20, 0 |
Решение. Составим систему линейных уравнений. Она будет иметь вид:
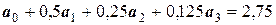
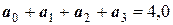
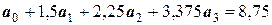
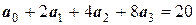 .
.
Применив способ единственного деления, выполним необходимые расчеты, занося результаты в таблицу 18.
Обратным ходом рассчитываем значения неизвестных:
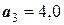 ;
; 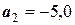 ;
; 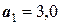 ;
; 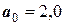 .
.
Искомый интерполяционный многочлен имеет вид:
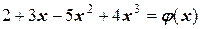 .
.
Таблица 18 - Решение задачи 16
| Шаг | Элементы матрицы | Свободный член | Множитель |
| 1, 0 0, 5 0, 25 0, 125 1, 0 1, 0 1, 0 1, 0 1, 0 1, 5 2, 25 3, 375 1, 0 2, 0 4, 0 8, 0 | 2, 75 4, 0 8, 75 20, 0 | 1, 0 | |
| 1 0, 5 0, 25 0, 125 | 2, 75 | -1; -1; -1 1/0, 5 | |
| 0 0, 5 0, 75 0, 875 0 1, 0 2, 0 3, 250 0 1, 5 3, 75 7, 875 | 1, 25 6, 0 17, 25 | ||
| 0 1 1, 5 1, 750 | 2, 50 | -1; -1, 5 1/0, 5 | |
| 0 0 0, 5 1, 5 0 0 1, 5 5, 25 | 3, 5 13, 50 | ||
| 0 0 1 3, 0 | 7, 0 | -1, 5 1/0, 75 | |
| 0 0 0 0, 75 | 3, 0 | ||
| 0 0 0 1 | 4, 0 |
Так как определитель системы имеет частный вид, разработаны алгоритмы нахождения коэффициентов интерполяционного многочлена, исключающие необходимость решения системы линейных уравнений. Рассмотрим два способа нахождения коэффициентов интерполяционного многочлена.