
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кусочно-полиномиальная аппроксимация. Сглаживание функции
|
|
В тех случаях, когда промежуток [ а, b ], на котором нужно подменить функцию f(x) функцией φ (х), велик и отсутствуют основания считать функцию f(x) достаточно гладкой при  , нет смысла пытаться повышать качество ее полиномиальной аппроксимации за счет использования в роли φ (х) многочленов высоких степеней. Более перспективным в этих условиях является применение кусочно-полиномиальной аппроксимации функции f(x). Предполагается, что функция φ (х) составляется из отдельных многочленов, как правило, одинаковой и невысокой степени, определенных каждый на своей части отрезка [ a, b ]. При этом, если функция f(x) непрерывна и имеется достаточное количество точечной информации о ней, можно рассчитывать приблизить ее на этом отрезке сколь угодно хорошо кусочно-полиномиальной функцией φ (х) только за счет увеличения числа частичных промежутков, составляющих данный отрезок, при любых фиксированных степенях составных многочленов и любых способах согласования f(x) и φ (х). Использование низких степеней многочленов, составляющих φ (х), позволяет легко находить их коэффициенты как из интерполяционных, так и из иных условий (например, аппроксимации методом наименьших квадратов).
, нет смысла пытаться повышать качество ее полиномиальной аппроксимации за счет использования в роли φ (х) многочленов высоких степеней. Более перспективным в этих условиях является применение кусочно-полиномиальной аппроксимации функции f(x). Предполагается, что функция φ (х) составляется из отдельных многочленов, как правило, одинаковой и невысокой степени, определенных каждый на своей части отрезка [ a, b ]. При этом, если функция f(x) непрерывна и имеется достаточное количество точечной информации о ней, можно рассчитывать приблизить ее на этом отрезке сколь угодно хорошо кусочно-полиномиальной функцией φ (х) только за счет увеличения числа частичных промежутков, составляющих данный отрезок, при любых фиксированных степенях составных многочленов и любых способах согласования f(x) и φ (х). Использование низких степеней многочленов, составляющих φ (х), позволяет легко находить их коэффициенты как из интерполяционных, так и из иных условий (например, аппроксимации методом наименьших квадратов).
Пусть функция f(x) задана таблично (см. таблицу 17). Требуется аппроксимировать ее функцией φ (х), выполняя условия интерполяции 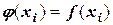 . Применим кусочно-линейную функцию φ (х) в виде:
. Применим кусочно-линейную функцию φ (х) в виде:
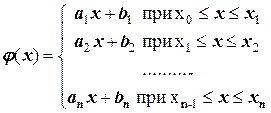 .
.
Иначе, нелинейная функция f(x) на всем отрезке заменяется линейными отрезками на каждом из п – участков (ломаная линия). В результате имеем п линейных уравнений, а соответственно п пар коэффициентов ak, bk (k=1, 2, …n). Они достаточно легко находятся, так как для каждого кусочно-линейного участка можно записать пару уравнений:
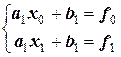 ;
; 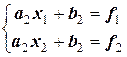 ; ….
; …. 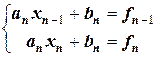
для участков 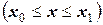 ;
; 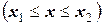 ; ….
; …. 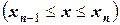 .
.
Нетрудно видеть, что коэффициенты уравнений можно рассчитать по формулам:
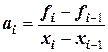 ;
; 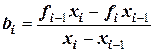 .
.
Аналогично функцию f(x) можно заменить кусочно-квадратичной функцией:
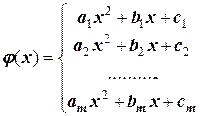 , где
, где 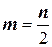 .
.
Очевидно, что, так как для определения уже трех неизвестных коэффициентов 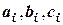 в квадратичных функциях требуются три уравнения типа (например, при п=4):
в квадратичных функциях требуются три уравнения типа (например, при п=4):
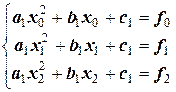 ;
; 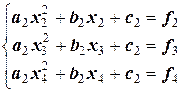
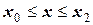 ;
; 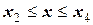 ,
,
то количество интервалов интерполирования п должно быть обязательно четным.
Фактически речь идет о последовательной линейной интерполяции по перемещаемым вдоль отрезка 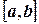 парам соседних узловых точек разбиения или о последовательной квадратичной интерполяции по тройкам таких точек.
парам соседних узловых точек разбиения или о последовательной квадратичной интерполяции по тройкам таких точек.
Задача 20. Для функции f(x), заданной таблично, выполнить кусочно-линейную и кусочно-квадратическую интерполяцию.
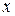
| 0, 5 | 1, 0 | 2, 0 | 3.0 | 4, 0 | 5, 0 | |
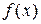
| 1, 5 | 2, 0 | 2, 0 | 1, 0 | 2, 0 |
Решение. Осуществляя линейное интерполирование на шести участках, запишем систему линейных уравнений:
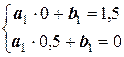 ;
; 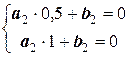 ;
; 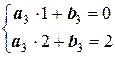
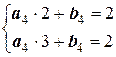 ;
; 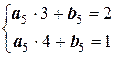 ;
; 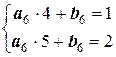 .
.
Из этих парных систем линейных уравнений получаем:
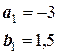 ;
;  ;
; 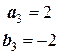 ;
; 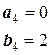 ;
; 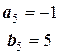 ;
; 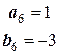 .
.
Тогда окончательно получаем кусочно-линейную интерполяционную функцию φ 1(х):

Кусочно-квадратичное интерполирование по тройкам известных точек отрезков 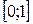 ;
; 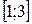 ;
; 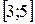 позволяет построить интерполяционную функцию φ 2(х):
позволяет построить интерполяционную функцию φ 2(х):
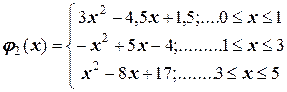 .
.
Графики функций φ 1(х) и φ 2(х) приведены на рисунках 20а, б, соответственно.
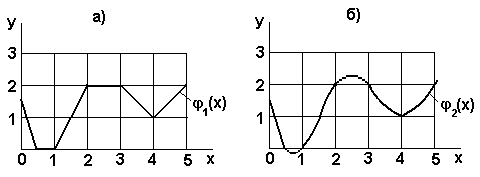
Рисунок 20 - Кусочно-интерполированные функции
Кусочно-линейная аппроксимация таблично заданных функций, проводимая на основе метода наименьших квадратов, приводит к понятию линейного фильтра. Рассмотрим общие представления о нем.
Предположим, что функция f(x) задается “длинной “ таблицей значениями fi(xi) на системе равноотстоящих точек 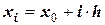 . Пусть также известно, что некоторые из значений f(x) могут содержать достаточно большие случайные ошибки (“выбросы“). Тогда, прежде чем производить какую-либо математическую обработку таких данных, целесообразно сначала произвести их сглаживание, чтобы уменьшить роль выбросов. Рассмотрим общий принцип одного из простейших подходов к такому сглаживанию.
. Пусть также известно, что некоторые из значений f(x) могут содержать достаточно большие случайные ошибки (“выбросы“). Тогда, прежде чем производить какую-либо математическую обработку таких данных, целесообразно сначала произвести их сглаживание, чтобы уменьшить роль выбросов. Рассмотрим общий принцип одного из простейших подходов к такому сглаживанию.
Если при кусочно-линейной интерполяции линейная функция на элементарном отрезке 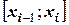 однозначно определялась по двум точкам из условия совпадения ее значений в них со значениями
однозначно определялась по двум точкам из условия совпадения ее значений в них со значениями 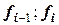 , то здесь рассматривается отрезок
, то здесь рассматривается отрезок 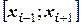 длиной 2h (т.е. включающий три опорные точки
длиной 2h (т.е. включающий три опорные точки 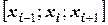 . На этом трехточечном отрезке функция f(x) подменяется приближением φ i(х), построенным по трем точкам, причем φ i(х) получают кусочно-линейной или кусочно-квадратической аппроксимацией методом наименьших квадратов (но не интерполяцией). Получив функцию φ i(х), вычисляют значение φ i(хi) и затем заменяют значение f(xi) значением φ i(хi). Перемещаясь таким образом по всему отрезку
. На этом трехточечном отрезке функция f(x) подменяется приближением φ i(х), построенным по трем точкам, причем φ i(х) получают кусочно-линейной или кусочно-квадратической аппроксимацией методом наименьших квадратов (но не интерполяцией). Получив функцию φ i(х), вычисляют значение φ i(хi) и затем заменяют значение f(xi) значением φ i(хi). Перемещаясь таким образом по всему отрезку 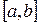 , т.е.варьируя i от 1 до (п-1), получают новую таблицу функции f(x). Безусловно, эту процедуру можно выполнить и для отдельных участков задания функции. Например, в таблице 20 экспериментальные точки
, т.е.варьируя i от 1 до (п-1), получают новую таблицу функции f(x). Безусловно, эту процедуру можно выполнить и для отдельных участков задания функции. Например, в таблице 20 экспериментальные точки 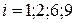 можно “улучшить“, применив подобную фильтрацию.
можно “улучшить“, применив подобную фильтрацию.
Описанная процедура называется осреднением по трем точкам и в зависимости от вида кусочной аппроксимации называется линейным или квадратическим фильтром. Большое значение процедура фильтрации (“ сглаживания“) играет в теории цифровой обработки сигналов (например, борьба с помехами в сигнале, повышение четкости изображения и т.д.). Отметим, что осреднение проводят и по большему числу точек, а иногда осуществляют двойную фильтрацию табличных данных. Однако при многократной (глубокой) фильтрации есть риск потерять полезную информацию о таблично заданной функции.