
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм симплекс-методу.
|
|
1. Симплекс-метод застосовується до канонічної задачі лінійного програмування, яка має вигляд:
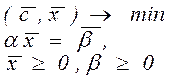 ,
,
де 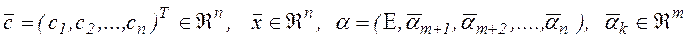 .
.
2. Знаходиться початковий базисний розв’язок (опорний план) 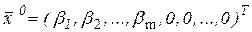 . Обчислюються відносні оцінки змінних:
. Обчислюються відносні оцінки змінних:
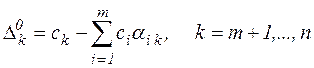 (для базисних змінних відносні оцінки рівні нулю). Отже, побудована початкова ітерація. Припустимо, що побудована s-та ітерація.
(для базисних змінних відносні оцінки рівні нулю). Отже, побудована початкова ітерація. Припустимо, що побудована s-та ітерація.
3. Проводиться аналіз відносних оцінок небазисних змінних:
- якщо всі відносні оцінки невід’ємні, то отриманий базисний розв’язок 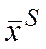 є оптимальним. Вихід з алгоритму;
є оптимальним. Вихід з алгоритму;
- якщо 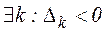 і
і 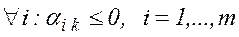 , то цільова функція (лінійна форма) необмежена знизу. Вихід з алгоритму;
, то цільова функція (лінійна форма) необмежена знизу. Вихід з алгоритму;
- якщо 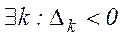 але
але  , то змінну
, то змінну 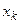 можна ввести в число базисних змінних. З числа базисних змінних виключається змінна
можна ввести в число базисних змінних. З числа базисних змінних виключається змінна 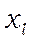 , де номер l знаходиться наступним чином l:
, де номер l знаходиться наступним чином l:  , індекс k шукається k:
, індекс k шукається k: 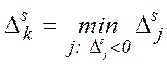 . При цьому коефіцієнти нової задачі обчислюються за формулами:
. При цьому коефіцієнти нової задачі обчислюються за формулами:
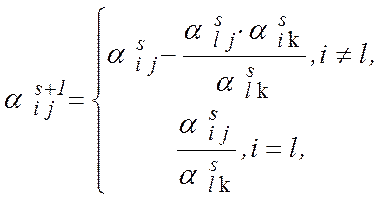

Новий базисний розв’язок буде: 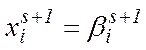 при цьому значення лінійної форми:
при цьому значення лінійної форми: 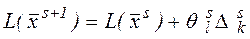 , зменшується на
, зменшується на  . Переходимо на початок п.3.
. Переходимо на початок п.3.
Завдяки тому, що кількість вершин скінчена на деякому кроці буде здійснюватись вихід із циклу.
Відомо, що симплекс-метод може бути використаний тільки для невироджених задач. Тобто, для задач в яких базисні розв’язки невироджені.
Зауваження. Розв’язок вироджений, якщо 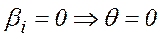 і метод зациклюється. Тобто, знаходимось в одній вершині, але міняємо базисні координати.
і метод зациклюється. Тобто, знаходимось в одній вершині, але міняємо базисні координати.
При розрахунках зручно користуватись симплекс-таблицями. Якщо задача канонічна, то таблиця має вигляд:
| № ітерації | базисні змінні | 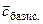
| 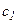
| 
| ... | 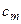
| ... | 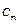
| 
| 
| Примітки |

| 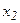
| ... | 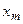
| ... | 
| ||||||

| 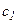
| ... | ... | 
| 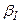
| ||||||
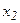
| 
| ... | ... | 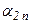
| 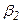
| ||||||
| ... | ... | ... | ... | ... | ... | ... | ... | ... | |||
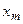
| 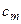
| ... | ... | 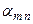
| 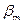
| ||||||
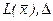
| 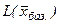
| ... | ... | 
|
Приклад. Нехай задано деяку стандартну задачу лінійного програмування:

Зведемо цю задачу до канонічного виду:
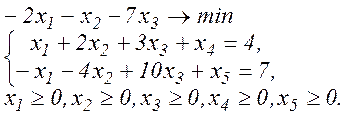
Цю задачу тепер можна розв’язати за допомогою симплекс-методу. Побудуємо симплекс-таблицю.
| № ітерації | базисні змінні | 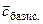
| -2 | -1 | -7 | 
| 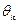
| Примітки | ||
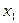
| 
| 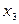
| 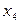
| 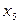
| ||||||
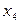
| 4/3 | 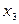 – ввести – ввести
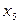 – вивести – вивести
| ||||||||
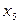
| -1 | -4 | 7/10 | |||||||
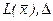
| -2 | -1 | -7 | |||||||
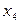
| 13/10 | 32/10 | -3/10 | 19/10 | 19/32 |  – ввести – ввести
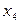 – вивести – вивести
| ||||
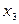
| -7 | -1/10 | -4/10 | 1/10 | 7/10 | - | ||||
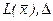
| -49/10 | -27/10 | -38/10 | 7/10 | ||||||

| -1 | 13/32 | 10/32 | -3/32 | 19/32 | 19/13 |  – ввести – ввести
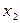 – вивести – вивести
| |||
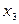
| -7 | 2/32 | 4/32 | 2/32 | 30/32 | 30/13 | ||||
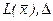
| -229/32 | -37/32 | 38/32 | 11/32 | ||||||

| -2 | 32/13 | 10/13 | -3/13 | 19/13 | |||||
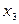
| -7 | -2/13 | 1/13 | 1/13 | 11/13 | |||||
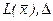
| -115/13 | 37/13 | 27/13 | 1/13 |
Всі відносні оцінки невід’ємні. Отже, знайдений розв’язок є оптимальним розв’язком канонічної задачі 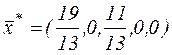 , при цьому оптимальний розв’язок початкової (заданої) задачі буде
, при цьому оптимальний розв’язок початкової (заданої) задачі буде 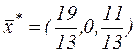 .
.
3. Симплексні перетворення. Відносні оцінки змінних. Критерій оптимальності базисного плану. Ознака необмеженості цільової функції. Алгоритм симплексного методу.
Ознака необмеженості цільової функції
Наведені у попередньому параграфі міркування складають основу симплекс-методу розв'язування ЗЛП.
Перш, ніж сформулювати алгоритм цього методу, доведемо декілька необхідних для його обгрунтування тверджень.
Теорема 1.4 (критерій оптимальності базисного розв'язку ЗЛП). Якщо для деякого базисного розв'язку 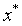 справджуються нерівності
справджуються нерівності 
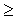 0,
0, 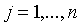 , то
, то 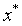 — оптимальний розв'язок ЗЛП.
— оптимальний розв'язок ЗЛП.
Доведення. Нехай для базисного розв'язку 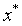 =(
=( 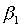 ,...,
,...,  , 0,..., 0), що визначається канонічною формою обмежень ЗЛП
, 0,..., 0), що визначається канонічною формою обмежень ЗЛП
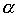
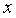 =
= 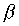 ,
, 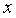
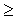 0,
0, 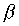
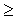 0,
0,
виконується умова теореми, тобто
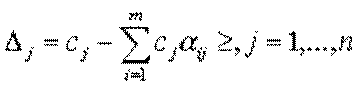 .
.
Ми повинні довести, що для будь-якого допустимого розв'язку  =(
=(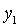 , …,
, …,  ) (
) ( 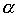
 =
= 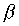 ,
, 
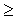 0) виконується нерівність
0) виконується нерівність 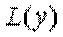
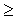
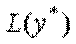 , а це і буде означати, що
, а це і буде означати, що 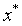 — оптимальний розв'язок ЗЛП.
— оптимальний розв'язок ЗЛП.
Дійсно, з умови теореми та з допустимості розв'язку  маємо
маємо
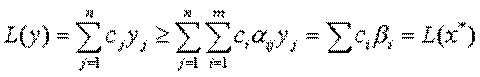 ,
,
що і доводить теорему.
Теорема 1.5 (критерій необмеженості цільової функції ЗЛП на допустимій множині). Якщо для деякого базисного розв'язку 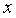 ЗЛП існує хоча б однеj, таке, що
ЗЛП існує хоча б однеj, таке, що  < 0 і вектор умов
< 0 і вектор умов  такий, що
такий, що 
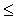 0, то цільова функція ЗЛП необмежена на допустимій множині, тобто
0, то цільова функція ЗЛП необмежена на допустимій множині, тобто
min 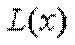 =
= 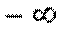 ,
, 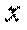
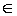
 .
.
Доведення. Нехай для базисного розв'язку 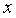 = (
= ( 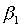 ,...,
,...,  , 0,..., 0), що визначається канонічною формою обмежень ЗЛП
, 0,..., 0), що визначається канонічною формою обмежень ЗЛП

виконується умова теореми  . Розглянемо вектор
. Розглянемо вектор

де  є j -ю координатою цього вектора і
є j -ю координатою цього вектора і  > 0. Покажемо, що
> 0. Покажемо, що 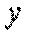

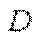 .
.
Дійсно, 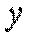 має невід'ємні координати
має невід'ємні координати 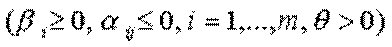 і задовольняє обмеження
і задовольняє обмеження 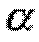
 =
= 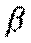 , що перевіряється безпосередньою підстановкою.
, що перевіряється безпосередньою підстановкою.
Обчислимо тепер значення цільової функції у точці 
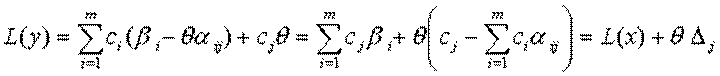 .
.
Через те, що 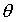 > 0 і
> 0 і  < 0 значення цільової функції можна необмежене зменшувати, залишаючись у допустимій області, що й завершує доведення теореми.
< 0 значення цільової функції можна необмежене зменшувати, залишаючись у допустимій області, що й завершує доведення теореми.