
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Двоїстий симплекс-метод.
|
|
Розглянемо метод розв'язування задач лінійного програмування, що базується на теорії двоїстості, i називається цей метод двоїстим симплекс-методом. Наведемо його обґрунтування.
Нехай розглядається СЗЛП:
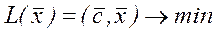
 (1)
(1)

Як відомо, двоїстою до задачі (1) є ЗЛП
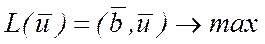
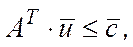 (2)
(2)
Нехай вектори умов 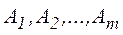 у задачі (1)є лінійно незалежними,
у задачі (1)є лінійно незалежними,  – базисна матриця. Спробуємо перейти від СЗЛП (1)до КЗЛП, для цього помножимо прямі обмеження
– базисна матриця. Спробуємо перейти від СЗЛП (1)до КЗЛП, для цього помножимо прямі обмеження 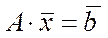 зліва на
зліва на  . Одержимо
. Одержимо 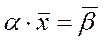 , де
, де 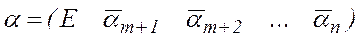 , Е – одинична матриця розмірності m × m. Якщо при цьому
, Е – одинична матриця розмірності m × m. Якщо при цьому  , то одержана ЗЛП є канонічною, якщо ж деякі компоненти вектора
, то одержана ЗЛП є канонічною, якщо ж деякі компоненти вектора 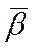 β від'ємні, то, звичайно, ні.
β від'ємні, то, звичайно, ні.
Означення 1. Майже канонічною задачею лінійного програмування (МКЗЛП) називається стандартна задача лінійного програмування (1), якщо матриця умов A містить одиничну матрицю.
Означення 2. Вектор 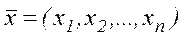 називається майже допустимим базисним розв'язком, якщо він задовольняє обмеження
називається майже допустимим базисним розв'язком, якщо він задовольняє обмеження 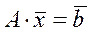 (але не обов'язково обмеженням
(але не обов'язково обмеженням 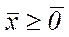 ) i його ненульовим компонентам відповідають лінійно незалежні вектори умов.
) i його ненульовим компонентам відповідають лінійно незалежні вектори умов.
Для одержаної задачі маємо  , вектори умов
, вектори умов 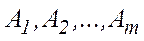 – лінійно незалежні,
– лінійно незалежні,  – базисна матриця. Змінні
– базисна матриця. Змінні  будемо називати базисними,
будемо називати базисними,  – небазисними. Надалі будемо розглядати лише ті майже допустимі базисні розв'язки (або ж ті МКЗЛП, що їх визначають), для яких відносні оцінки невід'ємні, тобто
– небазисними. Надалі будемо розглядати лише ті майже допустимі базисні розв'язки (або ж ті МКЗЛП, що їх визначають), для яких відносні оцінки невід'ємні, тобто 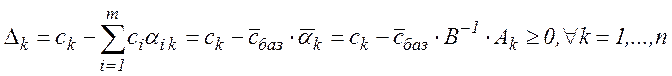 (3)
(3)
Для таких майже допустимих базисних розв'язківє очевидним критерій оптимальності: майже допустимий базисний розв'язок є оптимальним, якщо він є допустимим.
Зауважимо, що для майже допустимого базисного розв'язку, для якого виконується (3), вектор  є допустимим розв'язком двоїстої ЗЛП (
є допустимим розв'язком двоїстої ЗЛП (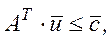 ). Отже, розглянемо МКЗЛ
). Отже, розглянемо МКЗЛ
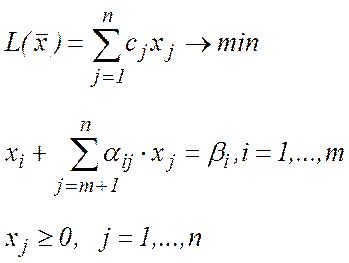
для якої 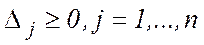 . Виключивши з цільової функції базисні змінні
. Виключивши з цільової функції базисні змінні  , маємо
, маємо
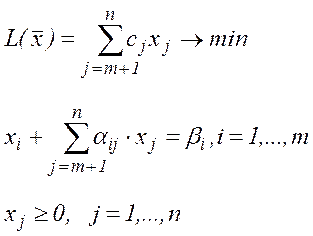 (4)
(4)
Двоїста до ЗЛП (4) має вигляд
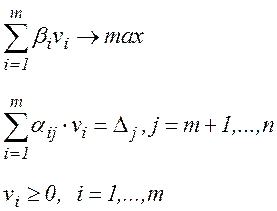
або, виконуючи заміну 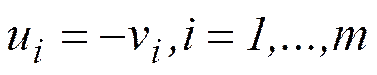
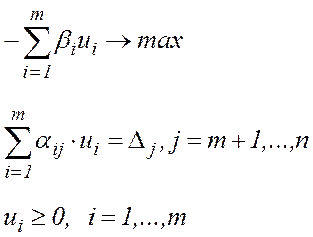
Останню задачу легко переводимо до канонічного вигляду, вводячи додаткові невід'ємні змінні  , та враховуючи, що максимiзацiя цільової функції еквівалентна мінімізації цієї ж функції з оберненим знаком:
, та враховуючи, що максимiзацiя цільової функції еквівалентна мінімізації цієї ж функції з оберненим знаком:
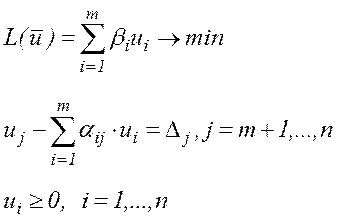 (5)
(5)
Отже, двоїстою до МКЗЛП (4) є КЗЛП (5). Зміст двоїстого симплекс-методу полягає у застосуванні звичайного симплекс-методу для розв'язування двоїстої ЗЛП (5). Оскільки метод, що розглядається, цікавить нас як метод розв'язування задачі (4), вияснимо, що означають для ЗЛП (4) перетворення кожної iтерацiї симплекс-методу, застосованого до задачі (5). Прямі обмеження КЗЛП (5) визначають базисний розв'язок цієї задачі – n -вимірний вектор  , для якого вектор
, для якого вектор 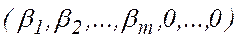 тієї ж вимірності є вектором симплекс-рiзниць. Якщо
тієї ж вимірності є вектором симплекс-рiзниць. Якщо 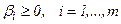 , то
, то  є оптимальним розв'язком задачі (5). Отже,
є оптимальним розв'язком задачі (5). Отже, 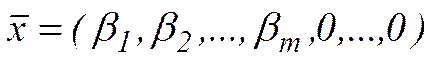 є оптимальним розв'язком ЗЛП (4) (критерій оптимальності майже допустимого базисного розв’язку). Інакше згідно симплекс-методу визначаються числа l та k з умов:
є оптимальним розв'язком ЗЛП (4) (критерій оптимальності майже допустимого базисного розв’язку). Інакше згідно симплекс-методу визначаються числа l та k з умов:
l: 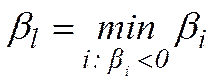 (6)
(6)
k: 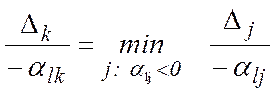 (7)
(7)
тобто, визначається ведучий елемент 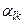 симплексного перетворення. Стосовно задачі (4) вказані дії також визначають ведучий елемент
симплексного перетворення. Стосовно задачі (4) вказані дії також визначають ведучий елемент 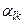 симплексного перетворення, при цьому з числа базисних виводиться вектор
симплексного перетворення, при цьому з числа базисних виводиться вектор 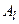 , а вектор
, а вектор 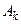 уводиться до числа базисних. Виконавши вказане перетворення, одержимо МКЗЛП, що визначає майже допустимий базисний розв’язок (аналогічно КЗЛП)
уводиться до числа базисних. Виконавши вказане перетворення, одержимо МКЗЛП, що визначає майже допустимий базисний розв’язок (аналогічно КЗЛП)
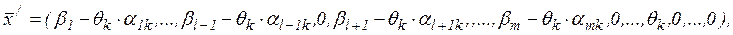
де 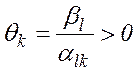 . З цього ж перетворення випливає також, що відносні оцінки
. З цього ж перетворення випливає також, що відносні оцінки  , для
, для  пов'язані з
пов'язані з  співвідношенням
співвідношенням
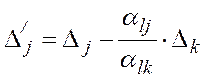 (8)
(8)
Враховуючи, що 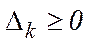 ,
, 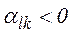 , робимо висновок, що при
, робимо висновок, що при 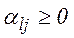 виконується
виконується 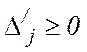 . Якщо ж
. Якщо ж  , то, записавши (7) у вигляді
, то, записавши (7) у вигляді 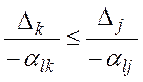 , маємо, що
, маємо, що 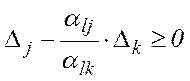 . Отже, для нового МДБР
. Отже, для нового МДБР 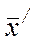 відносні оцінки також невід'ємні. Легко підрахувати також, що
відносні оцінки також невід'ємні. Легко підрахувати також, що 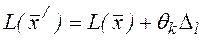 , тобто, при переході від точки
, тобто, при переході від точки 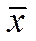 до
до 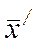 значення цільової функції збільшується, якщо
значення цільової функції збільшується, якщо  є невиродженим базисним розв'язком двоїстої ЗЛП i залишається незмінним у виродженому випадку.
є невиродженим базисним розв'язком двоїстої ЗЛП i залишається незмінним у виродженому випадку.
Зауважимо нарешті, що коли для деякого 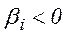 у задачі (5)
у задачі (5) 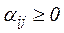 , то ця задача розв'язку не має через необмеженість цільової функції на допустимій множині, а задача (4) згідно теореми двоїстості не має розв'язку через те, що є порожньою її допустима множина. Все це дає можливість сформулювати алгоритм двоїстого симплекс-методу.
, то ця задача розв'язку не має через необмеженість цільової функції на допустимій множині, а задача (4) згідно теореми двоїстості не має розв'язку через те, що є порожньою її допустима множина. Все це дає можливість сформулювати алгоритм двоїстого симплекс-методу.
Алгоритм двоїстого симплекс-методу (ДСМ)
1.Зводимо вихідну ЗЛП до МКЗЛП i знаходимо її МДБР 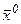 , для якого відносні оцінки невід'ємні.
, для якого відносні оцінки невід'ємні.
2.Нехай на s -ій iтерацiї маємо МКЗЛП, що визначає МДБР 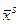 , якому відповідають невід'ємні відносні оцінки. Без обмеження загальності будемо вважати, що
, якому відповідають невід'ємні відносні оцінки. Без обмеження загальності будемо вважати, що 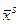 визначається системою прямих обмежень
визначається системою прямих обмежень
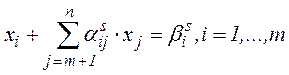 (9)
(9)
тобто, 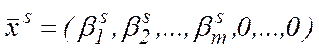 та
та 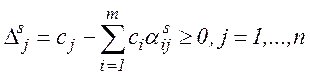
3. Якщо  , то здійснюється вихід із алгоритму:
, то здійснюється вихід із алгоритму:  є оптимальним розв'язком вихідної ЗЛП.
є оптимальним розв'язком вихідної ЗЛП.
4.Якщо існує принаймні одне 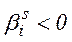 , таке, що
, таке, що  , то здійснюється вихід із алгоритму: вихідна ЗЛП розв'язку не має (її множина допустимих розв’язків є порожньою).
, то здійснюється вихід із алгоритму: вихідна ЗЛП розв'язку не має (її множина допустимих розв’язків є порожньою).
5. Знаходимо l з умови  . Отже, вектор
. Отже, вектор 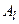 виводиться з числа базисних.
виводиться з числа базисних.
6. Знаходимо k з умови 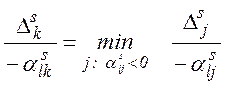 . Вектор
. Вектор 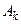 уводиться до числа базисних. Виконуємо симплексне перетворення над елементами розширеної матриці системи (9) з ведучим елементом
уводиться до числа базисних. Виконуємо симплексне перетворення над елементами розширеної матриці системи (9) з ведучим елементом 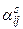 i повертаємось до пункту 2 алгоритму, заміняючи s на s+1.
i повертаємось до пункту 2 алгоритму, заміняючи s на s+1.