Теореми двоїстості.

Теорема 1. Якщо одна з пари двоїстих задач лінійного програмування має оптимальний розв'язок, то інша також має оптимальний розв'язок, причому оптимальні значення цільових функцій співпадають .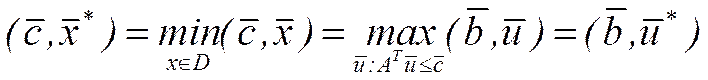

Теорема 2. Якщо цільова функція однієї з пари двоїстих задач лінійного програмування необмежена на допустимій множині (для задачі мінімізації – знизу, для задачі максимiзацiї – зверху), то інша задача не має допустимих розв’язків.

Зауваження до теореми 2. Цей факт невзаємний, тобто, якщо у однієї із задач не існує допустимих розв’язків, то це не означає, що цільова функція другої задачі необмежена.

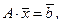Зауваження. Якщо задовольняє умову а відповідні відносні оцінки – невід’ємні, то є допустимим розв’язком для двоїстої задачі, причому необов’язкове обмеження .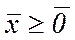

Двоїстий критерій оптимальності. Базисний розв'язок прямої задачі лінійного програмування є оптимальним тоді і лише тоді, коли існує вектор такий, що виконуються співвідношення

або в координатній формі