
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Побудова початкового базисного розв’язку.
|
|
1. Розглянемо задачу лінійного програмування: 
В кожному з непрямих обмежень стоїть “ 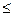 ”. Задача легко зводиться до канонічної задачі, шляхом введення в розгляд нових змінних
”. Задача легко зводиться до канонічної задачі, шляхом введення в розгляд нових змінних 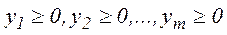 . Тоді отримаємо нові вектори
. Тоді отримаємо нові вектори 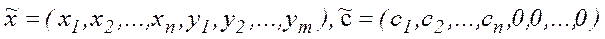 . Отже, наша задача набуде вигляду:
. Отже, наша задача набуде вигляду: 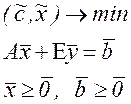
2. Розглянемо задачу лінійного програмування: 
В кожному з непрямих обмежень стоїть “ 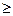 ”. Задача зводиться до канонічної задачі, шляхом введення в розгляд нових змінних
”. Задача зводиться до канонічної задачі, шляхом введення в розгляд нових змінних 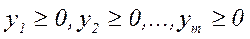 . Тоді
. Тоді 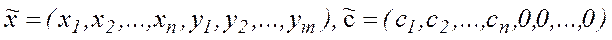 . Отже, наша задача набуде вигляду:
. Отже, наша задача набуде вигляду: 
Отриману задачу можна канонізувати, наприклад, таким чином:  , де l -те рівняння переписуємо без зміни, а i -те рівняння (
, де l -те рівняння переписуємо без зміни, а i -те рівняння (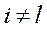 )замінюємо різницею між l -тим та i -тим рівнянням
)замінюємо різницею між l -тим та i -тим рівнянням 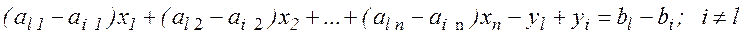
Задача майже канонізується (не вистачає l -го стовпчика, що відповідає уl). Пробуємо ввести в число базисних змінних змінну хк, таку що  , в k -ому стовпчику робимо нулі крім l -ого місця. Навіть якщо існує таке k, що
, в k -ому стовпчику робимо нулі крім l -ого місця. Навіть якщо існує таке k, що  , система може не канонізуватися, бо при виключенні
, система може не канонізуватися, бо при виключенні 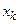 із рівнянь деякі праві частини можуть стати від’ємними. Отже, потрібно додати ще таку умову:
із рівнянь деякі праві частини можуть стати від’ємними. Отже, потрібно додати ще таку умову:  . В іншому випадку канонізувати не можна.
. В іншому випадку канонізувати не можна.
2.1. Метод штучної бази – це універсальний метод, який застосовується до стандартної задачі лінійного програмування:
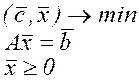
Для розв’язання даної задачі розглянемо нову задачу лінійного програмування (допоміжну):
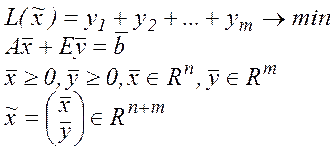
При розв’язанні такої задачі маємо, що  . Функція яка мінімізується – обмежена знизу.
. Функція яка мінімізується – обмежена знизу.
Маємо такі випадки:
a) 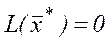
b) 
де 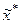 – оптимальний план допоміжної задачі.
– оптимальний план допоміжної задачі.
Теорема. Якщо  , то
, то 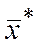 – опорний план (базисний розв’язок). Якщо хоча б одна із компонент
– опорний план (базисний розв’язок). Якщо хоча б одна із компонент  відмінна від нуля, наприклад
відмінна від нуля, наприклад  , то множина допустимих значень в початковій задачі порожня, тобто не існує розв’язків.
, то множина допустимих значень в початковій задачі порожня, тобто не існує розв’язків.
Недолік методу штучної бази в тому, що для знаходження базисного плану задачі потрібно повністю розв’язати нову задачу.
2.2. М-метод побудови базисного плану. Розглянемо разом із задачею лінійного програмування допоміжну задачу (М-задачу):
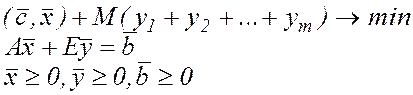
умова 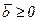 є неістотною.
є неістотною.
В цій задачі число М – невід’ємне і достатньо велике, більше ніж будь-які числа, які будуть зустрічатися в даній задачі.
Теорема. Якщо оптимальний розв’язок М-задачі має вигляд: 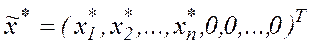 , то
, то 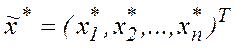 є оптимальним розв’язком початкової задачі.
є оптимальним розв’язком початкової задачі.
Наслідок. 1. Якщо в оптимальному розв’язку М-задачі хоча б одна компонента 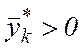 , то множина допустимих планів початкової задачі порожня.
, то множина допустимих планів початкової задачі порожня.
2. Якщо допоміжна задача не має розв’язку, в тому розумінні, що 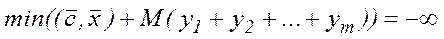 , то початкова задача теж не має розв’язку, в тому розумінні, що
, то початкова задача теж не має розв’язку, в тому розумінні, що 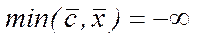 .
.
Приклад. Нехай задано деяку задачу лінійного програмування:
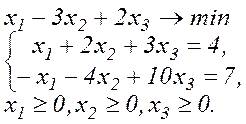
Допоміжна М-задача буде мати вигляд:

Ця задача тепер в канонічній формі, тому можна розв’язати її за допомогою симплекс-методу. Побудуємо симплекс-таблицю.
| № ітерації | базисні змінні | 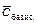
| -3 | М | М | 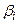
| 
| Примітки | ||

| 
| 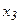
| 
| 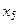
| ||||||

| М | 4/3 | 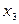 – ввести – ввести
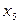 – вивести – вивести
| |||||||
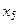
| М | -1 | -4 | 7/10 | ||||||

| 11 М | -3+2 М | 2-13 М | |||||||

| М | 13/10 | 32/10 | -3/10 | 19/10 | 19/32 |  – ввести – ввести
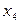 – вивести – вивести
| |||
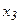
| -1/10 | -4/10 | 1/10 | 7/10 | - | |||||

| 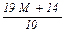
| 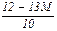
| 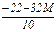
| 
| ||||||

| -3 | 13/32 | 10/32 | -3/32 | 19/32 | |||||
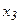
| 2/32 | 4/32 | 2/32 | 30/32 | ||||||

| 3/32 | 7/32 | 
| 
|
Всі відносні оцінки невід’ємні. Отже, знайдений розв’язок є оптимальним.  . Оскільки введені, допоміжні, змінні
. Оскільки введені, допоміжні, змінні  рівні нулю, то оптимальний розв’язок заданої (початкової) задачі буде:
рівні нулю, то оптимальний розв’язок заданої (початкової) задачі буде: 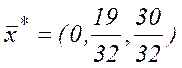 .
.
5. Двоїстість в ЛП. Несиметрична та симетрична пари двоїстих задач. Теореми двоїстості. Двоїстий симплекс-метод.
Одночасно із заданою задачею лінійного програмування вигідно розглядати двоїсту задачу лінійного програмування. Розглядаючи пару двоїстих задач, можна виписати за розв’язком однієї задачі розв’язок іншої.
Нехай задана стандартна задача лінійного програмування:

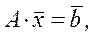
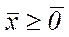
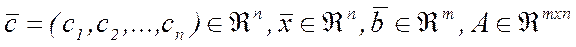 .
.
Цю задачу будемо називати прямою.
Двоїстою задачею до стандартної називається задача виду:

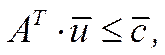
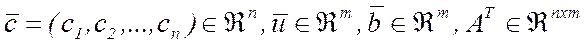 .
.
Зауважимо, що якщо пряма задача лінійного програмування має стандартну форму, то двоїста їй задача лінійного програмування не містить прямих обмежень на двоїсті змінні 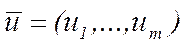 , тобто
, тобто  .
.
Щоб побудувати двоїсту до загальної задачі лінійного програмування, необхідно перетворити її до стандартної форми, а потім діяти згідно визначення двоїстої задачі.