Коефіцієнти парної кореляції. Кореляційна матриця

При побудові економетричної моделі залежності результативного показника від одного фактора щільність кореляційного зв’язку ми визначали з допомогою коефіцієнта кореляції. В багатофакторних економетричних моделях є коефіцієнти парної, частинної та множинної кореляції.

Коефіцієнти парної кореляції використовуються для вимірювання сили лінійних зв’язків різних пар змінних (ознак) із заданої множини. Значення парних коефіцієнтів кореляції між результативною змінною y та незалежними змінними x_j обчислюються за формулою:

, (2.16)

а між незалежними змінними x_l та x_j:

(2.17)

Парні коефіцієнти кореляції утворюють кореляційну матрицю (матрицю коефіцієнтів парної кореляції):

.

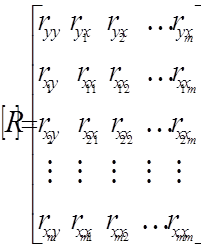Дана матриця є симетричною відносно головної діагоналі 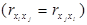, елементи якої рівні одиниці, тобто:

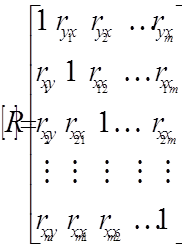. (2.18)

Припустимо, що змінна y залежить від двох факторів х₁ та х₂. Тоді ми будемо мати три коефіцієнти парної кореляції:

- коефіцієнт парної кореляції між y та х₁, або коефіцієнт кореляції економетричної моделі :

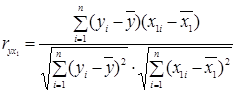; (2.19)

- коефіцієнт парної кореляції між y та х₂, або коефіцієнт кореляції економетричної моделі :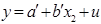

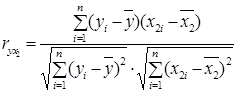; (2.20)

- коефіцієнт парної кореляції між незалежними змінними х₁ та х₂, або коефіцієнт кореляції економетричної моделі :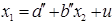

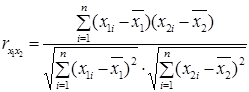. (2.21)

Кореляційна матриця матиме вигляд:

.

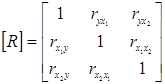Приклад 2.2. Використавши умову прикладу 2.1 знайти коефіцієнти парної кореляції.