Коефіцієнти множинної кореляції та детермінації

Основним показником тісноти кореляційного зв’язку між результативним показником y та всіма незалежними змінними 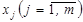, а також ступеня близькості вибраного виду математичної залежності до вибіркових даних є коефіцієнти множинної кореляції та детермінації.

Коефіцієнт множинної детермінації обчислюється за формулою:

,

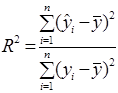Враховуючи рівність:

,

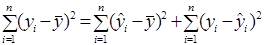маємо:

.

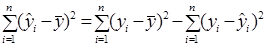Тоді вираз для R² прийме такий вигляд:

.

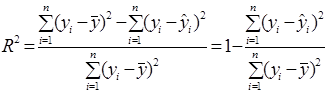З останньої формули випливає, що коли 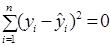, то 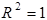. Отже, якщо всі вибіркові значення показника розміщені на лінії регресії, то коефіцієнт множинної детермінації дорівнює одиниці. А значить, чим ближче вибіркові значення наближаються до лінії регресії, тим ближче 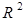наближається до одиниці, а отже, тим більше варіація залежної змінної визначається варіацією незалежних факторів. Як бачимо, коефіцієнт множинної детермінації показує частку варіації результативної ознаки, яка знаходиться під впливом досліджуваних факторів, тобто визначає, яка частка варіації ознаки y врахована в моделі та викликана впливом вибраних факторів. Його числове значення змінюється від нуля до одиниці, тобто 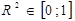. Якщо 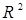прямує до нуля, то у вибірці відсутній лінійний зв’язок між залежною та незалежними змінними.

Характерною особливістю коефіцієнта детермінації 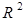є те, що він – неспадна функція від кількості факторів, які входять до моделі. Отже, якщо кількість незалежних факторів зростає, то значення 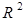так само зростає.

З останньої рівності маємо:

,

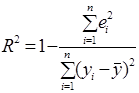причому значення знаменника у формулі не залежить від кількості факторів 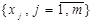, тоді як чисельник, навпаки, знаходиться у зворотній залежності. Тобто, при зростанні числа незалежних факторів, величина 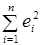спадає, або на крайній випадок не зростає.

Тому при співставленні між собою двох регресійних моделей для однакових залежних змінних, але з різною кількістю незалежних факторів, перевагу треба віддати тій моделі, для якої значення 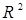є більшим.

Одним з основних показників тісноти кореляційного зв’язку результативного показника y з факторами 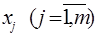, а також мірою ступеня відповідності даних 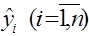є коефіцієнт множинної кореляції. Він визначається як коефіцієнт кореляції між y та 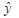має вигляд:

.

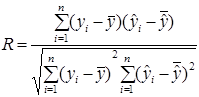Квадрат коефіцієнта множинної кореляції, як і випадку простої регресії є коефіцієнтом детермінації, тобто має місце .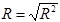

На практиці для обчислення значень коефіцієнтів множинної детермінації та кореляції, коли розраховані значення коефіцієнтів парної кореляції, використовують наступні формули:

- коефіцієнт множинної детермінації:

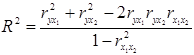. (2.23)

- коефіцієнт множинної кореляції: 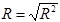. (2.24)

Приклад 2.5. Використавши дані прикладу 2.1 знайти коефіцієнт множинної детермінації та кореляції.

¨ Розв’язування.

Для знаходження коефіцієнта множинної детермінації використаємо формулу (2.23), використавши значення коефіцієнтів парної кореляції з прикладу 2.3:

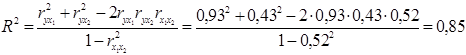а значить 85 % загальної дисперсії пояснюється залежністю обсягу валової продукції від вартості основних виробничих фондів та затрат праці. І тільки 15 % загальної дисперсії не може бути пояснено отриманою нами залежністю. Таким чином, можна зробити висновок, що побудована модель статистично значима.

Тоді коефіцієнт множинної кореляції буде:

,

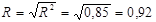а це означає, що між валовою продукцією та основними виробничими фондами і затратами праці існує тісний лінійний зв’язок.