Коефіцієнти частинної кореляції

Коефіцієнти частинної кореляції так само представляють лінійні зв’язки ознак, але при цьому береться до уваги чистий зв’язок пари ознак за умови, що зв’язки всіх інших ознак з ознаками із даної пари не діють. Отже, частинною кореляцією між ознаками х_i та x_j називається кореляційна залежність між цими ознаками при фіксованих значеннях інших ознак.

Нехай число незалежних змінних m=2. Для знаходження коефіцієнтів частинної кореляції використовуємо наступні формули:

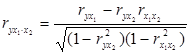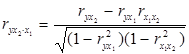, (2.22)

де 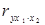– коефіцієнт частинної кореляції між змінними y та x₁ при виключенні впливу x₂. Він показує яку долю загальної дисперсії змінної y, що не пояснила змінна x₂ пояснить введення в економетричну модель змінної x₁.

– коефіцієнт частинної кореляції між змінними y та x₂ при виключенні впливу x₁. Він показує яку долю загальної дисперсії змінної y, що не пояснила змінна x₁ пояснить введення в економетричну модель нової змінної x₂.

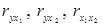– відповідно коефіцієнти парної кореляції.

Для m=3 маємо такі коефіцієнти частинної кореляції:

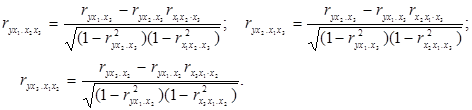
Узагальнюючи приведені вище формули для будь-якого числа пояснюючих змінних, отримаємо:

.

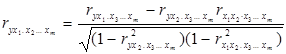Останнє співвідношення показує, що обчислення коефіцієнта частинної кореляції порядку m зводиться до визначення таких же коефіцієнтів, але порядку (m-1). Тому спочатку необхідно знайти коефіцієнти парної кореляції, а потім перейти до обчислення коефіцієнтів вищих порядків.

Приклад 2.4. Розрахувати коефіцієнти частинної кореляції на основі даних прикладу 2.1.