Класи нелінійних регресій

Розрізняють два класи нелінійних регресій:

1) І клас – це клас регресій, які нелінійні відносно пояснюючих змінних, але лінійні відносно оцінок параметрів економетричної моделі. Приклади таких функцій:

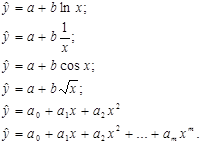
Цей клас нелінійних регресій ще називають квазілінійними регресіями, тому що їх можна привести до лінійного виду шляхом заміни, тобто лінеаризувати.

2) ІІ клас нелінійних регресій – це клас економетричних моделей, які нелінійні і відносно пояснюючої змінної (чи пояснюючих змінних) і відносно оцінок параметрів ЕМ. Приклади таких функцій:

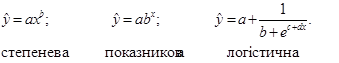
Такий клас регресій часто зустрічається при дослідженні економічних процесів чи явищ. Суттєвим його недоліком є те, що неможливо провести лінеаризацію та застосувати метод найменших квадратів.

Великий економічний інтерес серед функцій нелінійної регресії другого класу представляють виробничі функції.

Першою класичною виробничою функцією є степенева функція Кобба-Дугласа:

,

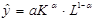де 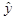– обсяг випуску продукції; К – затрати капіталу; L – затрати праці; a – коефіцієнт пропорційності; a - параметр функції або коефіцієнт еластичності по затратах праці.

Для загального випадку степенева функція Кобба-Дугласа має вигляд:

.

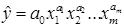де 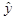– обсяг випуску продукції (національний дохід);

х₁, х₂, … х_m – фактори впливу на результативний показник;

a₁, a₂, … a_m – коефіцієнти еластичності.

Виробничі функції використовуються в двох аспектах: як самостійні економіко-математичні моделі для аналізу зв’язків між економічними показниками, прийняття рішень, прогнозування; як складові частини складніших моделей для оптимального планування та управління виробництвом. Нелінійні функції регресій І та ІІ класу інакше ще називають відповідно суттєво лінійними та суттєво нелінійними.