
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Перевірка значущості оцінок параметрів економетричної моделі
|
|
Значущість коефіцієнта множинної кореляції та оцінок параметрів економетричної моделі перевіряється аналогічно моделі парної регресії за t –критерієм Стьюдента.
Для оцінки значущості коефіцієнта множинної кореляції обчислюємо емпіричне значення параметру t:
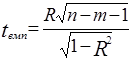 , (2.27)
, (2.27)
яке порівнюється з критичним значенням tкр, що знаходиться за таблицями розподілу Стьюдента при заданому рівні значущості a та k = n - m -1 ступенях вільності.
Правило використання критерію полягає у наступному:
- якщо 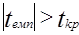 , то нульова гіпотеза Но на рівні значущості α відкидається і приймається альтернативна гіпотеза Н1 про існування залежності між змінними;
, то нульова гіпотеза Но на рівні значущості α відкидається і приймається альтернативна гіпотеза Н1 про існування залежності між змінними;
- якщо 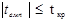 , то нульова гіпотеза Но на рівні значущості α приймається.
, то нульова гіпотеза Но на рівні значущості α приймається.
Перевірку нульових гіпотез стосовно параметрів b0, b1 та b2 економетричної моделі проводять аналогічно. Спочатку висуваємо нульові гіпотези:
H0: b0 =0, H0: b1 =0, H0: b2 =0.
Альтернативними будуть гіпотези:
H1: b0 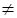 0, H1: b1
0, H1: b1 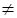 0, H1: b2
0, H1: b2 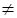 0.
0.
Потім обчислюємо емпіричні значення параметра t за формулами:
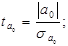
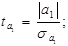
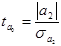 . (2.26)
. (2.26)
Емпіричне значення параметру порівнюють з критичним, знайденим за таблицями Стьюдента для заданого рівня значущості a та k = n - m -1 ступенів вільності. Якщо 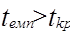 , то нульова гіпотеза Но із рівнем значущості α відкидається і приймається альтернативна гіпотеза Н1. Тоді відповідна оцінка вважається статистично значимою. Якщо ж
, то нульова гіпотеза Но із рівнем значущості α відкидається і приймається альтернативна гіпотеза Н1. Тоді відповідна оцінка вважається статистично значимою. Якщо ж 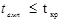 , то нульова гіпотеза Но для рівня значущості α приймається, а відповідна оцінка не є статистично знaчимою.
, то нульова гіпотеза Но для рівня значущості α приймається, а відповідна оцінка не є статистично знaчимою.
Приклад 2.7. На основі даних прикладу 2.1 виконати перевірки нульових гіпотез стосовно коефіцієнта кореляції та параметрів економетричної моделі.
¨ Розв’язування.
Висуваємо нульову гіпотезу Но: Rген =0 (робимо припущення, що коефіцієнт кореляції генеральної сукупності рівний нулю). Альтернативною гіпотезою буде Н1: Rген ¹ 0.
Далі для заданої вибірки з k=n - m -1 ступенями вільності обчислимо емпіричне значення критерію Стьюдента:
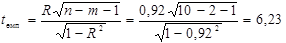
Для заданої ймовірності р =0, 9 (a =1- р=1-0, 9=0, 1) і k=10-2-1=7 ступенів вільності знаходимо табличне значення tкр.= 1, 89.
Оскільки 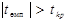 , то з надійністю р =0, 9 гіпотезу Но необхідно відкинути і прийняти альтернативну гіпотезу Н1 про існування залежності між змінними. Отже, у 90 % вибірок із генеральної сукупності коефіцієнт множинної кореляції не дорівнює нулю.
, то з надійністю р =0, 9 гіпотезу Но необхідно відкинути і прийняти альтернативну гіпотезу Н1 про існування залежності між змінними. Отже, у 90 % вибірок із генеральної сукупності коефіцієнт множинної кореляції не дорівнює нулю.
Далі виконаємо перевірку нульових гіпотез відносно b0, b1 та b2. Для цього спочатку обчислимо елементи дисперсійно-коваріаційної матриці, по головній діагоналі якої знаходяться дисперсії оцінок a0, a1 та а2, використавши формулу (2.14):
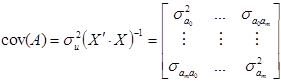 ,
,
а для обчислення дисперсії помилок формулу (2.15):
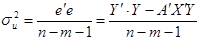 .
.
Елементи матриці 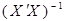 , векторів Y,
, векторів Y, 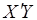 та А візьмемо з прикладу 2.1:
та А візьмемо з прикладу 2.1:
 ;
; 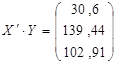 ;
; 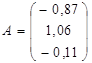 .
.
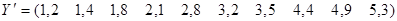 ;
;
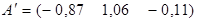 ;
;
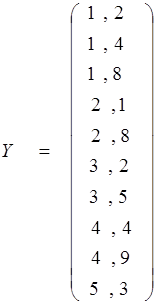
Тоді обчислимо 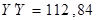 і
і 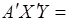 110, 2, а потім:
110, 2, а потім:
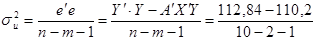 =0, 377.
=0, 377.
Перемноживши дисперсію помилок на діагональні елементи матриці 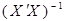 , отримаємо дисперсії оцінок, коренем з яких є середні квадратичні відхилення:
, отримаємо дисперсії оцінок, коренем з яких є середні квадратичні відхилення:
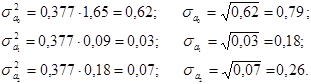
Дальше висуваємо гіпотезу Но: b0 =0 проти альтернативної Н1: b0 ¹ 0. Для цього знаходимо емпіричне значення за формулою:
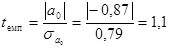
Оскільки емпіричне значення t менше критичного (tкр.= 1, 89), то нульова гіпотеза приймається і робиться висновок, що параметр b0 може бути рівним нулю в генеральній сукупності.
Перевіримо нульову гіпотезу Но: b1 =0. Обчислимо
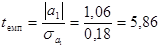 .
.
tемп> tкр, тому нульова гіпотеза відхиляється, значить b1 не може бути рівним нулю в генеральній сукупності, а отже оцінка a1, розрахована за даними вибірки, є статистично значимою.
Здійснимо перевірку нульової гіпотези стосовно параметру b2. Порахуємо
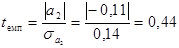 .
.
Оскільки емпіричне значення t менше критичного, то нульова гіпотеза приймається, значить параметр b2 може бути рівним нулю в генеральній сукупності, а отже оцінка a2, розрахована за даними вибірки, не є статистично значимою.