Метод неопределенных коэффициентов

Это метод отыскания частного решения линейного неоднородного уравнения с постоянными коэффициентами

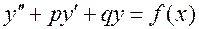
в случае, когда правая часть 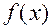имеет специальный вид, самая общая запись которого:

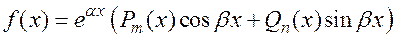, (26)

где 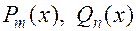– многочлены степен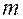и и 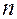соответственно:

.

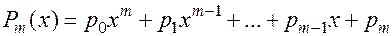
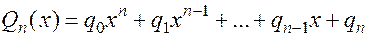Укажем характерные частные случаи функции (26).

1. 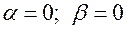. В этом случае правая часть 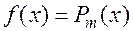является многочленом (поскольку 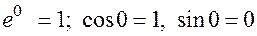). Например:

1)

;

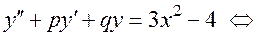
2)

.

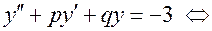
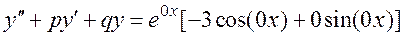2. 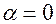. В этом случае 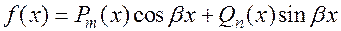. Например:

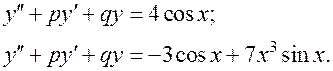
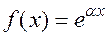3. . В этом случае . Например:

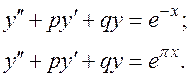
4. 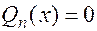. В этом случае . В частности, если степень многочлена 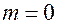, то многочлен является постоянным числом:

Например:

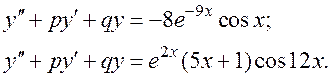
5. 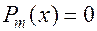. В этом случае 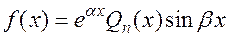. Например:

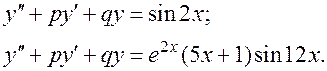
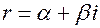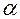Рассмотрим комплексное число , где и 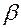берутся из записи (26) правой части 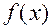неоднородного уравнения. Корни характеристического уравнения 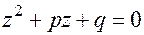записываются в виде

,

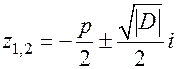где 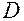– дискриминант уравнения.

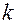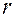Кратность числа как корня характеристического уравнения может иметь одно из трех значений:

1) 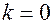; это означает, что 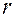не является корнем характеристического уравнения;

2) 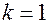; это означает, что 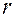является простым корнем характеристического уравнения; при этом дискриминант уравнения 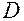отличен от нуля;

3) 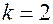, то есть 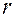— кратный корень; последнее возможно в том и только том случае, когда 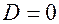; корень 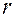при этом вещественный, так как его мнимая часть .

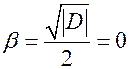На практике для определения кратности 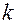нужно решить (квадратное) характеристическое уравнение и сравнить его корни с числом .

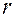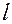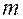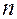Пусть – максимальная из степеней и многочленов 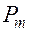и 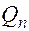в записи правой части (26).

Можно убедиться непосредственной подстановкой в дифференциальное уравнение, что функция

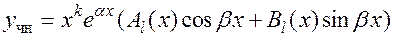, (27)

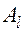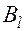где и – многочлены степени :

,

,

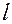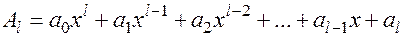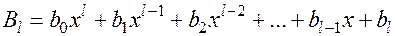при некоторых значениях коэффициентов 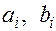этих многочленов является частным решением неоднородного уравнения. Для отыскания этих (неопределенных вначале) коэффициентов у функции (27) вычисляются первая и вторая производные; затем 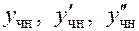подставляются в исходное уравнение, после чего приравниваются коэффициенты при одинаковых функциях-слагаемых обеих частей равенства. Это дает систему уравнений для отыскания коэффициентов .

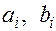В итоге отыскание частного решения проводится по следующему алгоритму:

1. Нахождение корней характеристического уравнения.

2. Определение величин .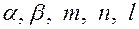

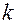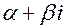3. Выявление кратности числа как корня характеристического уравнения.

4. Запись частного решения 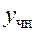в виде (27) с неопределенными коэффициентами многочленов .

5. Вычисление производных .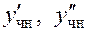

6. Подстановка 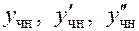в дифференциальное уравнение.

7. Приравнивание коэффициентов при одинаковых функциях в обеих частях равенства.

8. Решение получившейся системы уравнений, получение коэффициентов многочленов .

9. Запись частного решения с найденными коэффициентами.

После этого можно записать общее решение в виде

Примеры. 1. Рассмотрим уравнение .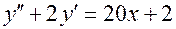

Выполняем последовательно инструкции алгоритма:

1. . Общее решение соответствующего однородного уравнения: .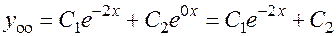

2. Находим параметры правой части:

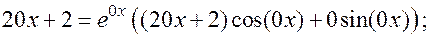
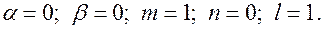
3. 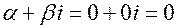; кратность .

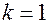4. .

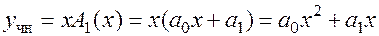5. .

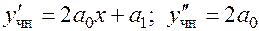6. Подставляем в уравнение: .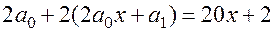

7. ;

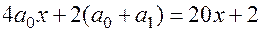8. ; .

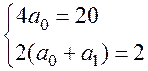9. .

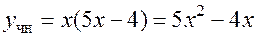Общее решение неоднородного уравнения:

.

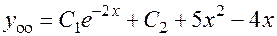2. Рассмотрим уравнение

.

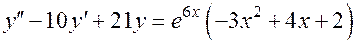Выполняем последовательно инструкции алгоритма:

1. . Общее решение соответствующего однородного уравнения: .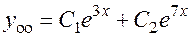

2. Находим параметры правой части:

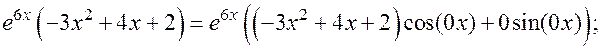
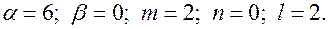
3. 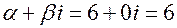; кратность .

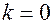4. ;

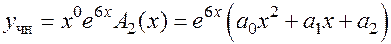5.

;

.

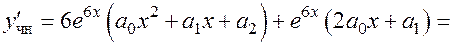
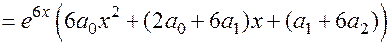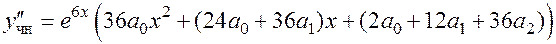6. Подставляем в уравнение:

.

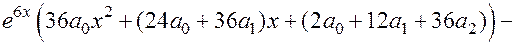
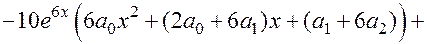
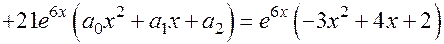7. Приводим подобные члены и приравниваем коэффициенты 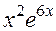при

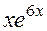, при и при :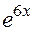

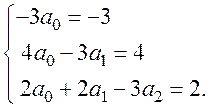
8. Решаем систему: .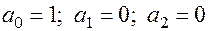

9. .

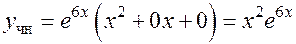Общее решение неоднородного уравнения:

.

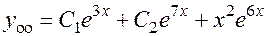3. Рассмотрим уравнение .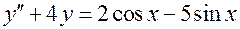

1. 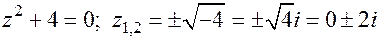. Общее решение соответствующего однородного уравнения:

.

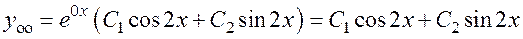2. Находим параметры правой части:

;

.

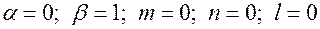3. 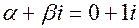; кратность .

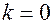4. ;

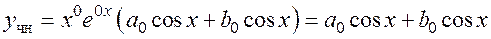5. ;

.

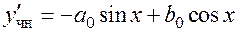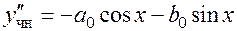6. Подставляем в уравнение:

;

.

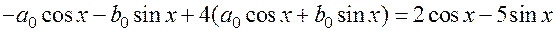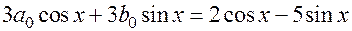7. Приравниваем коэффициенты 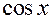при и при :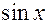

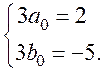
8. .

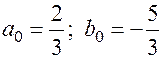9. .

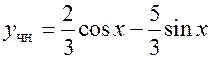Общее решение неоднородного уравнения:

.

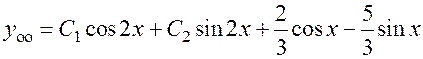ЛИТЕРАТУРА

1. Пискунов Н.С. Дифференциальное и интегральное исчисления, т. 1-2.- Интеграл-Пресс, 2005. – 416 с.

2. Данко П.Е. и др. Высшая математика в упражнениях и задачах,

часть 1, 2. М.: " Оникс 21 век". – 2003.

3. Волков Н.И., Голоскоков П.Г., Шкадова А.Р. Матрицы, опреде-

лители и системы линейных уравнений. Учебное пособие. – СПб.:

СПбГУВК. – 2006.

4. Ястребов М.Ю. Производная и исследование функций. СПб.: СПГУВК, 2003. – 45 с.

5. Ястребов М.Ю. Неопределенный и определенный интегралы. СПб.: СПГУВК, 2004. – 55 с.

6. Ястребов М.Ю. Функции нескольких переменных. СПб.: СПГУВК, 2006. – 48 с.

7. Лащенов В.К. Комплексные числа. СПб.: СПГУВК, 2010. – 8 с.

СОДЕРЖАНИЕ

	Исходные понятия…………………………………………..
	Начальные условия и задача Коши………………………...
	Общее решение и общий интеграл………………………...
	Метод разделения переменных…………………………….
	Однородное уравнение первого порядка………………….
	Линейное уравнение первого порядка…………………….
	Уравнения, допускающие понижение порядка…………...
7.1	Уравнение вида ………………………………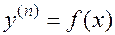
7.2	Уравнение, не содержащее явно неизвестную функцию …………………………………………………..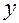
7.3	Уравнение, не содержащее явно независимую переменную ………………………………………………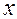
	Линейное уравнение второго порядка……………………..
8.1	Основные понятия…………………………………………..
8.2	Свойства решений однородного линейного уравнения…..
8.3	Линейное уравнение с постоянными коэффициентами…..
8.4	Структура общего решения неоднородного линейного Уравнения……………………………………………………
	Метод вариации произвольных постоянных (метод Лагранжа)……………………………………………
	Метод неопределенных коэффициентов…………………..
	Литература…………………………………………………..