Несобственные интегралы I и II рода.

Несобственный интеграл 1-го рода:

Пусть функция f(x) непрерывна [а; ∞).

Определение 1. Несобственные интегралы от функции f(x) в [a; +∞) называется

– несобственный интеграл, то есть

.

Геометрический смысл несобственного интеграла состоит в том, что , выражает площадь неограниченной (бесконечной), заключённой между линиями y=f(x), где х-является Осью абсцисс.

Аналогично определение несобственного Интеграла и для других бесконечных интегралов:

А) ;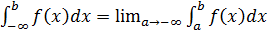

Б) .

Несобственные интегралы 2-го ряда:

Определение 2. Несобственные интегралы от ф-ции f(x) непрерывны в [a; в) и неограниченной при х-> в-0(левосторонний предел), называется

Если указанный предел существует и конечен, то интеграл несобственный, называется сходящимся, в обратном случае - расходящимся.

.

Если f(x) непрерывна (а; в), [a; c), (c; b].

.
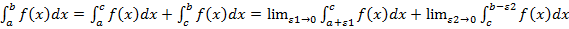