Двойной интеграл в полярных координатах. Приложения двойного интеграла.

Двойной интеграл в полярных координатах
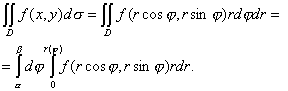Пусть область D ограничена линией r = r() и лучами = и =, где и r – полярные координаты точки на плоскости, связанные с ее декартовыми координатами x и y соотношениями (рис. 5). В этом случае Замечание. Если область D в декартовых координатах задается уравнением, содержащим бином , например, и т.д., то вычисление двойного интеграла по такой области удобнее производить в полярных координатах. приложения дв.интеграла:
Наименование величины	Общее выражение	Прямоугольные координаты	Полярные координаты
Площадь плоской фигуры
Масса тонкой плоской пластинки плотностью
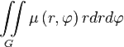
Площадь куска поверхности
Объем цилиндрического тела, стоящего наплоскости
Момент инерции плоской фигуры относительно оси
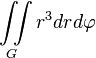
Момент инерции плоской фигуры относительно оси
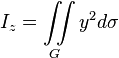
Координаты центра масс однородной пластинки
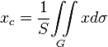
Примечания	1) Область — проекция на плоскость ; в каждую точку области проектируется только одна точка поверхности; — угол между касательной плоскостью и плоскостью . 2) Совмещенной с плоскостью . 3) Или, что то же, относительно центра О.