Свойства оператора набла

Этот вектор приобретает смысл в сочетании со скалярной или векторной функцией, к которой он применяется.

Если умножить вектор на скаляр , то получится вектор

, который представляет собой градиент функции .

Если вектор скалярно умножить на вектор , получится скаляр

, то есть дивергенция вектора .

Если умножить на векторно, то получится ротор вектора .

Также, произведение есть оператор Лапласа, и обозначается . В декартовых координатах оператор Лапласа определяется следующим образом:

.

Поскольку оператор набла является дифференциальным оператором, то при преобразовании выражений необходимо учитывать как правила векторной алгебры, так и правила дифференцирования. Например:

К простейшим векторным полям относятся: соленоидальное, потенциальное и гармоническое.

Определение 1: Векторное поле называется соленоидальным или трубчатым, если во всех точках поля
Соленоидальное поле не имеет ни источников, ни стоков, его векторные линии замкнуты. Поскольку div\vec{B}=0, то поле вектора магнитной индукции является соленоидальным.

Определение 2: Векторное поле называется потенциальным или безвихревым, если во всех точках поля
Для потенциального векторного поля всегда найдется такая скалярная функция u(M) (потенциал векторного поля ), что .
Потенциал векторного поля можно найти по формуле

где – произвольная точка поля, в которой функции P, Q, R определены, С – произвольная постоянная.

Определение 3: Векторное поле называется гармоническим, если во всех точках поля и
и т.е. поле является соленоидальным и потенциальным.

25.Задача об объёме цилиндрического тела. Определение и вычисление двойного интеграла. Основные свойства.

Рассмотрим тело, ограниченное сверху поверхностью снизу - замкнутой областью D плоскости Оху, с боков - цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 5). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z=ƒ (х; у) на плоскость Оху) произвольным образом на п областей Di, площади которых равны Рассмотрим цилиндрические столбики с основаниями Di, ограниченные сверху кусками поверхности z=ƒ (х; у) (на рис. 5 один из них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием D_i через ∆ V_i, получим

Возьмем на каждой площадке D_i произвольную точку M_i(x_i;, y_i) и заменим каждый столбик прямым цилиндром с тем же основанием D; и высотой z_i=ƒ (х_i; у_i).

Объем этого цилиндра приближенно равен объему Δ V_i цилиндрического

столбика, т. е. . Тогда получаем:

Это равенство тем точнее, чем больше число n и чем меньше размеры «элементарных областей» D_i. Естественно принять предел суммы (7.3) при условии, что число площадок D_i неограниченно увеличивается (n -> ∞), а каждая площадка стягивается в точку (maxd_i-> 0), за объем V цилиндрического тела, т. е.

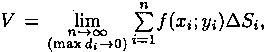
или, согласно равенству (7.2),

Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.

Определение:

Двойным интегралом от функции по ограниченной замкнутой области называется предел интегральной суммы, построенной для функции при неограниченном увеличении числа разбиений области на ячейки ( ) и при стягивание каждой ячейки в точку ( ), если такой предел существует и не зависит от способа разбиения области на ячейки, ни от выбора в каждой из них.

Теорема существования:

Для всякой непрерывной функции в ограниченной замкнутой области существует двойной интеграл:

Свойства двойного интеграла:

3) Если область разбить линией на две области и такие, что , а пересечение и состоит лишь из линии, их разделяющей, то:

4) Если в области имеет место неравенство , то и . Если в области функции и удовлетворяют неравенству, то и

6) Если функция непрерывна в замкнутой области , площадь которой , то , где 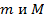– соответственно наименьшее и наибольшее значения подынтегральной функции в области .

7) Если функция непрерывна в замкнутой области , площадь которой , то в этой области существует такая точка , что . Величину называют средним значением функции в области

Вычисление двойного интеграла:
Интеграл функции , вычисляемый по двумерной области . Область разбивается на малые части. Эти малые части характеризуются их площадями и длинами наибольшего отрезка, который можно провести внутри частичной области. Этот отрезок называется диаметром частичной области. В каждой частичной области выбирается точка 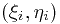, и составляется интегральная сумма
. Затем осуществляется переход к пределу разбиения области на бесконечно малые частичные области, а именно требуют, чтобы длина самого большого диаметра частичной области стремилась к нулю. Величина предела и является интегралом