Тройной интеграл. Определение, свойства и вычисление.

Определение. Тройным интегралом от функции F(x, y, z) по пространственной области Ω (омега) наз. предел, к которому стремится n-нная интегральная сумма , при стремлении к нулю наибольшего диаметра частичных областей

Вычисление тройного интеграла

· В декартовых координатах:

Пусть z=

Z=

· В цилиндрических координатах:

dV=dxdydz=rdrd

· Сферические координаты:

Формулы перехода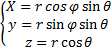

dV=dxdydz=

Основные свойства тройного интеграла:

Пусть функции f (x, y, z) и g (x, y, z) интегрируемы в области U. Тогда справедливы следующие свойства:

1.

2.

3. , где k - константа;

4. Если в любой точке области U, то

5. Если область U является объединением двух непересекающихся областей U ₁ и U ₂, то;

6. Пусть m - наименьшее и M - наибольшее значение непрерывной функции f (x, y, z) в области U. Тогда для тройного интеграла справедлива оценка:

где V - объем области интегрирования U.

7. Теорема о среднем значении тройного интеграла.
Если функция f (x, y, z) непрерывна в области U, то существует точка M ₀ U, такая, что

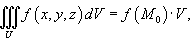где V - объем области U.