Частные производные I и II порядка функции двух переменных. Касательная плоскость и нормаль к поверхности.

Рассмотрим функцию двух переменных .Зафиксируем значение одного из ее аргументов, например , положив 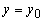. Тогда функция есть функция одной переменной . Пусть она имеет производную в точке :

.

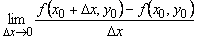Данная производная называется частной производной (или частной производной первого порядка) функции по в точке и обозначается одним из следующих символов: ; ; ; .

Разность называется частным приращением по функции в точке и обозначается символом :

.

Учитывая приведенные обозначения, можно записать

.

Аналогично определяются и обозначаются частное приращение функции по и частная производная по в точке :

,

.

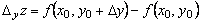Значение частной производной зависит от точки , в которой она вычисляется. Поэтому частная производная функции двух переменных , вообще говоря, есть функция точки , т.е. также является функцией двух переменных и .

Все правила и формулы дифференцирования, выведенные для производных функций одной переменной, сохраняются для частных производных функции двух переменных.

Однако следует помнить, что при нахождении частной производной по какому-либо аргументу второй аргумент считается постоянным.

Заметим, что частные производные функции являются функциями тех же переменных. Эти функции, в свою очередь, могут иметь частные производные, которые называются вторыми частными производными (или частными производными второго порядка) исходной функции.

Например, функция имеет четыре частных производных второго порядка, которые обозначаются следующим образом:

; ;

; .

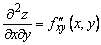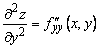При этом частные производные и называются смешанными частными производными.

Обратите внимание на то, что . Данный результат не случаен, так как имеет место следующая теорема.

Теорема 7.1. Две смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности.

Пусть поверхность задана в неявном виде: F(x, y, z)=0 и пусть точка M0(x0, y0, z0) принадлежит данной поверхности. Тогда уравнение касательной плоскости к этой поверхности в точке M0 таково:

F′ x(M0)⋅ (x− x0)+F′ y(M0)⋅ (y− y0)+F′ z(M0)⋅ (z− z0)=0(1)

Уравнение нормали имеет вид: x− x0F′ x(M0)=y− y0F′ y(M0)=z− z0F′ z(M0)(2)

Если же уравнение поверхности задано в явном виде z=f(x, y), то уравнение касательной плоскости имеет вид: f′ x(x0, y0)⋅ (x− x0)+f′ y(x0, y0)⋅ (y− y0)− (z− z0)=0(3)

Уравнение нормали в случае явного задания поверхности таково: x− x0f′ x(x0, y0)=y− y0f′ y(x0, y0)=z− z0− 1(4)

4… Определение: Плоскость, в которой распложены все касательные к линиям на поверхности, проходящим через точку касания M₀, называется касательной плоскостью к поверхности в точке M₀.

Определение: Нормалью к поверхности называется прямая перпендикулярная касательной плоскости и проходящая через точку касания.

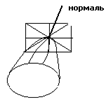Так как нормаль перпендикулярна касательной плоскости, то в качестве направляющего вектора можно взять вектор нормали к касательной плоскости (координаты вектора нормали - это частные производные.)

Тогда уравнение нормали имеет вид: ;

То есть если уравнение поверхности задано в виде z=f(x, y), точка M₀(x₀, y₀) и f(x₀, y₀) принадлежат поверхности, точка M₀ – точка касания, тогда уравнение касательной плоскости имеет вид: .

А в случае поверхности, заданной уравнением вида F(x, y, z)=0, уравнение касательной плоскости имеет вид: , где

точка M₀(x₀, y₀, z₀) – точка касания.

Каноническое уравнение прямой в пространстве