Функциональные ряды. Степенные ряды. Теорема Абеля о сходимости степенного ряда. Радиус сходимости и интервал сходимости степенного ряда.

①

Ряд вида ① называется функциональным, если его члены являются функцией x.

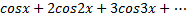
Ряд вида ① может для одних значений x- сходится, а для других x- расходится. Значение x=x₀ при котором при котором функциональный ряд сходим, называется точкой схождения ряда.

Совокупность всех точек сходимости ряда называется областью сходимости ряда.

Степенным рядом называется функциональный ряд вида ②.

② , где , … 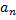- коэффициент степенного ряда, если то

③

Теорема Абеля: Если степенной ряд сходим при x=x₀ (x₀≠ 0), то он абсолютно сходится для любых x, где .

Следствия из теоремы: Если степенной ряд расходится при x=x₀, то он расходится и при всяком x, где .

Из теоремы Абеля вытекает, что для каждого степенного ряда имеющего точки сходимости и расходимости существует такое положительное число R, что при < R ряд сходится абсолютно, а при > R ряд расходится.

Радиусом сходимости степенного ряда ② называется такое число n, что < R ряд сходится, а для > R ряд расходится.

а) Если ряд расходится при всех x кроме нуля, то будем считать, что R=0.

б) Если ряд сходится при любых x, то R =

1)

2)

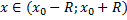
Формула радиуса сходимости:

Формула радиуса расходимости:

14.Основные свойства степенных рядов: теоремы о непрерывности суммы степенного ряда, почленном дифференцировании и интегрировании степенных рядов.

1) Сумма степенного ряда есть функция непрерывности в интервале сходимости ряда:

2) Степенной ряд можно почлено интегрировать в интервале сходимости ряда:

3) Степенной ряд можно почлено дифференцировать на интервале сходимости: