Разложение функций в степенные ряды. Ряд Тейлора. Ряд Маклорена.

Представление функции в виде

(6.1)

называется ее разложением в степенной ряд.

Теорема 6.1. Если функция f(x) раскладывается в окрестности точки х0 в степенной ряд (6.1) с радиусом сходимости R, то:

1. функция f имеет на интервале (x0 – R, x0 + R) производные всех порядков, которые можно найти почленным дифференцированием ряда (6.1): (6.2)

2. (6.3)

3. ряды (6.1), (6.2) и (6.3) имеют одинаковые радиусы сходимости.

Доказательство всех трех утверждений следует из общих свойств степенных рядов (теоремы 5.2 и 5.3).

Теорема 6.2. Если функция f раскладывается в некоторой окрестности точки х0 в сте-пенной ряд (6.1), то , и, следовательно, справедлива формула

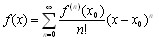(6.4)

Доказательство.

Дифференцируя т раз равенство (6.1), получим:

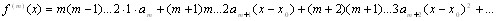
Примем х = х0, тогда f(m)(x0) = m! am, что доказывает формулу (6.4).

Следствие. Если в некоторой окрестности заданной точки функция раскладывается в степенной ряд, то это разложение единственно.

Действительно, из теоремы 6.2 следует, что коэффициенты степенного ряда могут иметь только вид, задаваемый формулой (6.4).

Определение 6.2. Пусть функция f(x) определена в некоторой окрестности точки х0 и имеет в этой точке производные всех порядков. Тогда ряд

называется рядом Тейлора.

Пример. Найдем разложение в ряд Тейлора при х0 = 0 функции f(x) = 2x.

. Следовательно,

.

Определение 6.3. Если при разложении в ряд Тейлора принимается х0 = 0, то полученный ряд 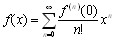(6.5)

называется рядом Маклорена (см. предыдущий пример).

Разложение в степенной ряд некоторых элементарных функций.

В лекции 21 (1-й семестр) рассматривалось представление функции в виде многочлена Тейлора с остаточным членом. Поскольку коэффициенты ряда Тейлора и многочлена Тейлора вычисляются по одной и той же формуле, мы можем воспользоваться прове-денными в лекции 21 вычислениями для получения разложения в ряд Тейлора некото-рых элементарных функций. При этом обратим особое внимание на определение обла-сти сходимости полученных рядов.

1. 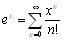. Сходимость полученного ряда исследовалась в примере 2 лекции 5, где показано, что он абсолютно сходится при любом х.

2. .

3. .

Используя формулу Даламбера для определения радиуса сходимости, найдем, что он равен бесконечности, то есть функции y = sin x и y = cos x раскладываются в ряд Тей-лора на всем множестве действительных чисел.

4. . Запишем остаточный член этой формулы в форме Лагранжа:

, и исследуем его поведение при 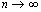для | x| < 1,

| x | > 1 и | x | = 1. При | x| < 1 , при | x | > 1 . Поэтому по теоре-ме 1.5 при | x| < 1 ряд сходится, а при | x | > 1 расходится. При х = -1 ряд расходится, так как представляет собой гармонический ряд, все члены которого имеют знак «-», а при х = 1 получаем знакопеременный ряд, сходящийся условно по признаку Лейбница. Следовательно, областью сходимости полученного ряда является интервал (-1, 1].

5. . Найдем радиус его сходимости по формуле Даламбера: Следовательно, интервал сходимости – (-1, 1).

16.Разложение основных элементарных функций в степенной ряд: y=e^x, y=sinx, y=cosx, y=(1+x)^m.

Основные (табличные) разложения. Выпишем их:

Утверждение. При разложении функции в ряд Тейлора используются основные (табличные) разложения и действия над рядами. Радиус сходимости ряда может быть получен по виду раскладываемой функции без использования формулы общего члена ряда и формул для нахождения радиуса. Радиус сходимости ряда, полученного при разложении данной функции в окрестности точки , равен расстоянию от центра разложения — точки до ближайшей особой точки функции. Если функция является аналитической всюду, то .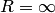

17. Теорема об условиях разложения функций в ряд Тейлора. Применение степенных рядов в приближённых вычислениях.

Функция, аналитическая в области , в окрестности каждой точки этой области представляется в виде степенного ряда, радиус сходимости 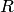которого не меньше, чем расстояние от точки до границы области . Коэффициенты ряда вычисляются по формуле

где — произвольный контур, принадлежащий области и охватывающий точку , в частности, — окружность или по формуле

Применение степенных рядов в приближённых вычислениях.В приближенных вычислениях степенные ряды играют большую роль. С помощью рядов были составлены таблицы тригонометрических функций, таблицы логарифмов, таблицы значений других функций, которые применяются в различных областях знаний.

Вычисление значений тригонометрических функций. С помощью степенных рядов можно приближенно вычислять значения функций sinx и cosx. Чем больше абсолютные значения х, тем больше членов разложения необходимо взять, чтобы получить значения sinx или cosx с заданной точностью. Три малых значения х можно считать

Чтобы решить сколько членов разложения следует взять, надо оценить остаток ряда. Так как ряды sinx и cosx знакочередующиеся, то остаток по абсолютной величине не превосходит первого отброшенного члена. Поэтому отбрасывают все члены, начиная с того, который по абсолютной величине меньше заданной погрешности вычисления.

С помощью степенных рядов и формул приведения составляются таблицы значений тригонометрических функций. sin63⁰=cos27⁰.

Приближенное извлечение корней.