
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение функции двух переменных. Область определения и область значений. Способы, функции задания. Предел и непрерывность функции переменных.
|
|
Функция двух переменных. Способы задания.
Область определения
Если каждой паре (х, у) значений двух независимых друг от друга переменных величин х и у из некоторой области их изменения D соответствует определенное значение величины z, то говорят, что z является функцией от x и y в области D.
Символически функция двух переменных обозначается так:
 .
.
Как и функция одной переменной она может быть задана аналитически, таблично и графически. Переход от одного способа задания к другому осуществляется по тем же правилам, что и для функции одной переменной.
Если на плоскости самая простая и самая изученная линия – это прямая, то наиболее простая поверхность в пространстве – это плоскость, уравнение которой в общем виде записывается так:

Разделив обе части равенства на D, получим равносильное уравнение

где 
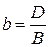 ,
,  . Его называют уравнением плоскости «в отрезках».
. Его называют уравнением плоскости «в отрезках».
По полученному уравнению легко изобразить плоскость в декартовой системе координат. Найдем точки ее пересечения с осями координат: с осью ОХ: 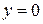 ,
, 
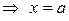 , с осью ОY:
, с осью ОY:  ,
, 
 , и с осью ОZ:
, и с осью ОZ:  ,
, 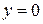
 . Соединим полученные точки, продолжая их во все стороны, и получим изображение плоскости.
. Соединим полученные точки, продолжая их во все стороны, и получим изображение плоскости.
Для нашего случая 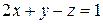 ,
,  ,
,  ,
,  . Построим эту плоскость по точкам
. Построим эту плоскость по точкам

В разделе «Аналитическая геометрия» мы также изучили кривые второго порядка – окружность, эллипс, гиперболу и параболу. В трехмерном пространстве они перешли в сферу, эллипсоид, гиперболоид (однополостный и двуполостный) и параболоид. В сечении этих тел плоскостями, параллельными координатным плоскостям, получаются все те же окружность, эллипс и т.д. Но на этом дело не закончилось. Кривые, вырвавшись в трехмерное пространство, создали эллиптический гиперболоид, гиперболический параболоид, конические и цилиндрические поверхности. Как и в случае одной переменной, функция двух переменных существует не при любых значениях х и у.
Определение Совокупность пар значений (х, у), при которых определяется функция  , называется областью определения или областью существования этой функции.
, называется областью определения или областью существования этой функции.
Область определения наглядно иллюстрируется геометрически, как совокупность точек, принадлежащих плоскости ХОY. Именно она называется областью определения функции. В дальнейшем мы будем рассматривать области, ограниченные некоторыми линиями. Эти линии называются границами области. Точки, не лежащие на границе, называют внутреннимиточками области. Область, состоящая только из внутренних точек, называется незамкнутой, или открытой. Если к области относятся и точки границы, то ее называют замкнутой.Область называется ограниченной, если существует такое положительное число С, что расстояние любой точки  плоскости от начала координат О(0, 0) меньше С, т.е.
плоскости от начала координат О(0, 0) меньше С, т.е.  .
.
Предел и непрерывность функции переменных.
При рассмотрении предела функции одной переменной было введено понятие окрестности точки. Под окрестностью точки 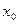 Принимался интервал, содержащий эту точку. При введении понятия предела функции двух переменных Принимался интервал, содержащий эту точку. При введении понятия предела функции двух переменных  будем рассматривать окрестность точки в плоскости будем рассматривать окрестность точки в плоскости  .
Окрестностью точки .
Окрестностью точки 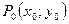 Называется внутренность круга с центром в этой точке. Если радиус круга равен Называется внутренность круга с центром в этой точке. Если радиус круга равен  , то говорят о , то говорят о  -окрестности точки -окрестности точки  . Очевидно, что любая точка . Очевидно, что любая точка 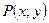 , принадлежащая , принадлежащая  -окрестности точки -окрестности точки 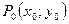 , находится от этой точки на расстоянии, меньшем , находится от этой точки на расстоянии, меньшем  .
Число .
Число  называется Пределом функции двух переменных называется Пределом функции двух переменных  при при  , если для любого числа , если для любого числа  найдется такая найдется такая  -окрестность точки -окрестность точки 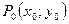 , что для любой точки , что для любой точки 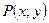 этой окрестности (за исключением, быть может, точки этой окрестности (за исключением, быть может, точки  ) имеет место неравенство ) имеет место неравенство  , или , или  .
При этом пишут .
При этом пишут  или или  , так как при , так как при  , очевидно, , очевидно, 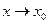 , ,  .
Заметим, что если число .
Заметим, что если число  Есть предел функции Есть предел функции  , то как это следует из определения предела, разность , то как это следует из определения предела, разность  является бесконечно-малой, когда точка Произвольным образом (по любому направлению) неограниченно приближается к точке является бесконечно-малой, когда точка Произвольным образом (по любому направлению) неограниченно приближается к точке  .
Функция двух переменных называется Бесконечно-малой при .
Функция двух переменных называется Бесконечно-малой при 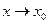 , ,  , если ее предел равен нулю, т. е. , если ее предел равен нулю, т. е. 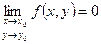 .
Понятие Непрерывности функции нескольких переменных устанавливается с помощью понятия предела.
Функция нескольких переменных .
Понятие Непрерывности функции нескольких переменных устанавливается с помощью понятия предела.
Функция нескольких переменных 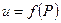 называется Непрерывной в точке называется Непрерывной в точке  , если , если 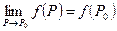 .
Заметим, что функция .
Заметим, что функция 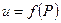 , непрерывная в точке , непрерывная в точке  , должна быть определена в этой точке и некоторой ее окрестности (иначе нельзя было бы осуществить переход к пределу). Точка , должна быть определена в этой точке и некоторой ее окрестности (иначе нельзя было бы осуществить переход к пределу). Точка  , в которой функция нескольких переменных , в которой функция нескольких переменных 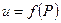 непрерывна, называется Точкой непрерывности функции.
Для непрерывных в точке функций справедлива следующая теорема.
Теорема. Если функции непрерывна, называется Точкой непрерывности функции.
Для непрерывных в точке функций справедлива следующая теорема.
Теорема. Если функции 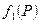 и и  непрерывны в точке непрерывны в точке  , то в этой точке непрерывны и их сумма , то в этой точке непрерывны и их сумма  , разность , разность  и произведение и произведение 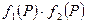 ; если, кроме того, ; если, кроме того,  , то частное , то частное  также есть непрерывная функция в точке также есть непрерывная функция в точке  .
Если условие непрерывности нарушено (или функция не определена, или не существует предел, или не выполняется равенство), точка называется Точкой разрыва. Точки разрыва могут быть изолированными или образовывать Линии разрыва.
Функция .
Если условие непрерывности нарушено (или функция не определена, или не существует предел, или не выполняется равенство), точка называется Точкой разрыва. Точки разрыва могут быть изолированными или образовывать Линии разрыва.
Функция  Называется Непрерывной в области, если она непрерывна в каждой точке этой области.
Теорема. Если функция Называется Непрерывной в области, если она непрерывна в каждой точке этой области.
Теорема. Если функция  непрерывна в ограниченной замкнутой области непрерывна в ограниченной замкнутой области  , то она в этой области:
1. ограничена: , то она в этой области:
1. ограничена:  ;
2. имеет наименьшее ;
2. имеет наименьшее 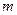 и наибольшее и наибольшее 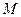 Значения: Значения:
 ;
3. принимает хотя бы в одной точке области любое численное значение, заключенное между ;
3. принимает хотя бы в одной точке области любое численное значение, заключенное между 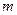 и и 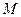 . .
|