Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Моделирование структуры конкурентной экономики
|
|
5.4.1. Построение базовой модели одно-продуктового рынка с двумя производителями и потребителями (модель 2*2)
В настоящее время, как показано в разделе 5.1, рыночные структуры подразделяются на совершенную (чистую) и несовершенную конкуренцию: в т. ч. на монополистическую конкуренцию, олигополию, монополию и монопсонию. Для перечисленных типов рыночных структур используем, представленную в разделе 5.3.1, математическую модель одно - продуктового рынка:
opt F (X (t))= { F 1(X (t)) = { max fq (X (t)) = 
pqxql (t), q= 
}, (5.4.1)
F 2(X (t))={ min fl (X (t)) = 
pqxql (t), l= 
}}, (5.4.2)
b 
£ pqxql £ b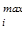 
, l= , (5.4.3)
aqxql (t)£ bq, q= , (5.4.4)
p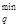 
£ pq £ p 
, xql(t) ³ 0, q= , l= , (5.4.5)
Обозначения см. выше.
Для анализа сформулированных рыночных структур рассмотрим представленную модель для наиболее простой ситуации, когда на рынке с одним товаром действуют два производителя и два потребителя этого продукта, хотя модель позволяет анализировать и более крупные. Наиболее близки к такой модели - модели дуополии Курно, Штакельберга, Бертрана и Эджуорта [3, 53], в которых рассмотрены взаимоотношения только двух производителей (фирм).
Введем обозначения:
x 1, x 2 - объемы продукта проданные первым, x3, x4 - вторым производителем первому и второму потребителю соответственно;
p 1, p 2, p 3, p 4 - цены на продукт фиксированы, что позволяет рассматривать представленную задачу как линейную;
a 1, a 2, a 3, a 4 - затраты на производство продукта у обоих производителей;
pq= cq - aq - прибыль от производства и продажи продукта у обоих производителей q =1, 2;
b 
, b 
, l =1, 2 - минимальный и максимальный объем финансовых средств, которые могут выделить на покупку продукта от разных фирм первый и второй потребитель.
bq - финансовые возможности фирмы при производстве продукта, q =1, 2.
Базовую математическую модель рынка с двумя производителя и двумя потребителями (модель 2*2) в линейной постановке, (т. е. цены на некоторый период времени постоянны) с учетом введенных обозначений, представим в виде векторной задачи линейного программирования:
opt F (X)={ max f 1(X) = p1 x 1 + p2 x 2, ma x f 2(X) = p3 x 3 + p4 x 4, (5.4.6)
min f 3(X) = p 1 x 1 + p 3 x 3 , min f 4(X) = p 2 x 2 + p 4 x 4}, (5.4.7)
при ограничениях
b 
≤ p 1 x 1 + p 3 x 3 ≤ b 
, b 
≤ p 2 x 2 + p 4 x 4 ≤ b 
, (5.4.8)
a 1 x 1+ a 2 x 2 ≤ b 1, a 3 x 3 + a 4 x 4 ≤ b 2, (5.4.9)
x 1, x 2, x 3, x 4 ³ 0. (5.4.10)
Математическая модель рынка (5.4.6)-(5.4.10) может использоваться для различных рыночных структур, путем изменения соответствующих параметров, поэтому она названа базовой. Аналогично могут быть построены базовые модели большей размерности.
Для решения векторной задачи (5.4.6)-(5.4.10) используем алгоритмы, основанные на основе нормализации критериев и принципе гарантированного результата, представленные в четвертой части. Решение задачи (5.4.6)-(5.4.10) рассмотрим при равнозначных критериях и заданном приоритете критерия.
В модели такого рынка в зависимости от изменения параметров модели - цены на товар и ресурсных затрат можно рассматривать:
· модель совершенной конкуренции, т. е. модель с одинаковыми параметрами;
· модель олигополии, в которой параметры могут изменяться, т. е. у некоторых фирм имеется возможность доминирования над другими фирмами по ценам ресурсам и прочим параметрам:
· модель монополии, в которой имеется один критерий (5.4.6) производителей и множество критериев (5.4.7) потребителей;
· модель монопсонии, в которой имеется и множество критериев (5.4.6) производителей и один критерий (5.4.7) потребителя.