
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение модели рынка
|
|
Рассматривается рынок с одним товаром, который в соответствии с определением раздела 5.1 представим в виде трех подсистем:
· производители в совокупности, определяющие рыночное предложение;
· потребители, определяющие рыночный спрос;
· третья связующая подсистема – товар.
Первая подсистема представлена Q производителями, вторая - L потребителями этого продукта: Q – число, q - индекс, а Q º  - множество индексов производителей (фирм), аналогично l - индекс, L - число, L - множество потребителей, l =
- множество индексов производителей (фирм), аналогично l - индекс, L - число, L - множество потребителей, l =  .
.
Математическая модель рынка должна отражать цели участников рынка и ограничения, накладываемые на их деятельность, а также учитывать внешнее окружение, которое может быть определено функциями спроса и предложения. Поэтому рассмотрим два варианта модели рынка:
· общая модель рынка, т. е. без учета функции спроса-предложения;
· модель рынка, учитывающая функции спроса-предложения.
Математическую модель одно - продуктового рынка (1 вариант) с учетом целей всех потребителей и производителей продукта, а также ограничений, накладываемых на их финансовые возможности (бюджет) и ресурсы, представим в виде векторной задачи математического программирования (ВЗМП):
opt F (X (t))= { F 1(X (t)) = { max fq (X (t)) =  pqxql (t), q=
pqxql (t), q=  }, (5.3.1)
}, (5.3.1)
F 2(X (t))={ min fl (X (t)) =  pqxql (t), l=
pqxql (t), l=  }}, (5.3.2)
}}, (5.3.2)
b  £
£  pqxql £ b
pqxql £ b 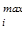 , l=
, l=  , (5.3.3)
, (5.3.3)
 aqxql (t)£ bq, q=
aqxql (t)£ bq, q=  , (5.3.4)
, (5.3.4)
p 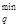 £ pq £ p
£ pq £ p  , xql(t) ³ 0, q=
, xql(t) ³ 0, q=  , l=
, l=  , (5.3.5)
, (5.3.5)
где F (X (t)) - векторная целевая функция (векторный критерий), в ней K = Q È L - множество критериев - потребителей и производителей соответственно;
pq = pq - aq, q=  - прибыль производителей, определяющаяся разностью между ценой продажи pq и затратами aq;
- прибыль производителей, определяющаяся разностью между ценой продажи pq и затратами aq;
pq, xql, q=  , l=
, l=  - управляющие переменные, они представлены в задаче произведением, из этого вытекает, что задача векторной оптимизации (5.3.1)-(5.3.5) - нелинейная;
- управляющие переменные, они представлены в задаче произведением, из этого вытекает, что задача векторной оптимизации (5.3.1)-(5.3.5) - нелинейная;
в (5.3.1) F 1(X (t))- векторный критерий Q производителей, которые максимизируют прибыль от производства и продажи отдельного вида товаров;
в (5.3.2) F 2(X (t))- векторный критерий L потребителей, которые минимизируют свои затраты, за счет стоимости на покупаемую продукцию;
(5.3.3) - ограничения по бюджетным (финансовым) возможностям L потребителей, а (5.3.4) - ограничения по производственным мощностям Q производителей;
(5.3.5) - ограничения, определяющие пределы изменения стоимости единицы товара, установленные на рынке, и ограничения, связанные с не отрицательностью объемов произведенной и проданной продукции.
Задача (5.3.1)-(5.3.5) представляет модель одно - продуктового рынка на дискретный период t Î T.
Для решения векторной задачи математического программирования (5.3.1)-(5.3.5) используются методы, основанные на нормализации критериев и принципе гарантированного результата, которые дают возможность решать задачи при равнозначных критериях и заданном приоритете критерия, представленные в девятой главе.
В результате решения задачи (5.3.1)-(5.3.5) - модели одно - продуктового рынка при равнозначных критериях получим:
· точку оптимума Хo= { x  , p
, p  , q=
, q=  , l=
, l=  }, которая складывается из двух составляющих: x
}, которая складывается из двух составляющих: x  - объемы продукта, произведенного и проданного каждым производителем каждому потребителю, p
- объемы продукта, произведенного и проданного каждым производителем каждому потребителю, p  - стоимости, которая удовлетворяет требованиям, как производителей, так и потребителей за период времени tÎ T;
- стоимости, которая удовлетворяет требованиям, как производителей, так и потребителей за период времени tÎ T;
· величины целевых функций в точке Xo: fk (Xo), k=  , K=Q È L, в т. ч. fq (Xo), q=
, K=Q È L, в т. ч. fq (Xo), q=  , определяют доходы каждого производителя; f l(Xo), l =
, определяют доходы каждого производителя; f l(Xo), l =  , определяют затраты каждого покупателя;
, определяют затраты каждого покупателя;
· суммарный объем продаж всех производителей и финансовых затрат всех потребителей, которые равны между собой:
få q(X)= 
 (pql+aql) x
(pql+aql) x  =få l (X) =
=få l (X) = 
 p
p  x
x  , (5.3.6)
, (5.3.6)
т. е. суммарное предложение få q(X) равно суммарному спросу få l(X), заметим, что состояние рынка, при котором спрос равен предложению, называется равновесным, а цена, при которой достигается равенство спроса и предложения, называется равновесной ценой, т. е. p  - равновесная цена;
- равновесная цена;
· величины целевых функций fk(Xo), k=  , выраженные относительно своих оптимумов X
, выраженные относительно своих оптимумов X  , т. е.
, т. е.
l k (Xo) = (fk (Xo) -f  )/(f
)/(f  -f
-f  ), k=
), k=  , (5.3.7)
, (5.3.7)
где lk(Xo), k=  , XoÎ S - нормализованный критерий, в котором f
, XoÎ S - нормализованный критерий, в котором f  -наилучшее решение по k Î K критерию, f
-наилучшее решение по k Î K критерию, f  - наихудшее соответственно, K = Q È L - множество критериев;
- наихудшее соответственно, K = Q È L - множество критериев;
· максимальную относительную оценку lo, которая является максимальным нижним уровнем, и до которого подняты обоюдные интересы всех производителей и потребителей в относительных единицах l k (X o), k =  , другими словами, lo является гарантированным результатом, который гарантирует, что в полученной оптимальной точке Xo все критерии в относительных единицах (оценки производителей и потребителей) равны или лучше lo: l k (Xo)³ l o или
, другими словами, lo является гарантированным результатом, который гарантирует, что в полученной оптимальной точке Xo все критерии в относительных единицах (оценки производителей и потребителей) равны или лучше lo: l k (Xo)³ l o или
lo £ l k (Xo), k =  , Xo Î S. (5.3.8)
, Xo Î S. (5.3.8)
Любое увеличение интересов (критерия) какого-либо производителя или потребителя, приводят к ухудшению оставшихся участников рынка (производителей и потребителей), т. е. точка { Xo, l o} оптимальна по Парето.
Вектор - функция F1 (X) = { fq (Xo), q=  } представляет собой функцию предложения, а вектор - функция F 2(X) = { fl (Xo), l=
} представляет собой функцию предложения, а вектор - функция F 2(X) = { fl (Xo), l=  } представляет функцию спроса.
} представляет функцию спроса.