
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нелинейная модель рынка
|
|
Методологию моделирования рынка с учетом функции спроса и предложения проведем в три этапа: постановка задачи, построение модели вида (5.3.1)-(5.3.5) и непосредственно моделирование.
Постановка задачи.
Дано. Предположим, что известны статистические данные о покупках и производстве телевизионных приемников: спрос (цена - объемы покупок), предложение (цена - объемы продаж) [26], т. е. решается задача в условиях неопределенности.
На объем производства и соответственно продаж оказывают влияние:
· производственные возможности производителей: a 1= a 2=400 - затраты на производство продукта у обоих производителей, b 1 =b 2 = 150000 - финансовые возможности фирм при производстве продукта;
· финансовые возможности потребителей: b  = 100000, b
= 100000, b 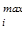 = 300000, " l Î L – минимальный и максимальный объем финансовых средств, которые они может выделить на покупку продукта от разных фирм. Максимальная цена, которую в состоянии оплатить потребители, pmax =800.
= 300000, " l Î L – минимальный и максимальный объем финансовых средств, которые они может выделить на покупку продукта от разных фирм. Максимальная цена, которую в состоянии оплатить потребители, pmax =800.
Построить оптимизационную модель рынка с учетом функций спроса и предложения и рассчитать оптимальную цену, объемы спроса-предложения.
Построение модели рынка с учетом функции спроса и предложения выполним за два шага: используя статистические данные, сформируем функции спроса и предложения, на их основе построим модель вида (10.1)-(10.5).
Построим функцию спроса и предложения, проведя регрессионный анализ статистических данных с использованием пакета программ Statistica [8]. В результате расчета получим: средние значения цены и объемы реализуемого товара, а также данные регрессионного анализа, в т. ч. функции линейного спроса и предложения:
q  = – 2, 60 сх + 1631, 47, q
= – 2, 60 сх + 1631, 47, q  = 2, 11 сх -566, 07. (5.3.17)
= 2, 11 сх -566, 07. (5.3.17)
Эти уравнения и соответствующие параметры регрессионного анализа показаны на рис. 5.2, 5.3.
Построим модель рынка, для этого, используя исходные данные, преобразуем задачу математического программирования (5.3.1)-(5.3.5) с учетом функций рыночного спроса и предложения (5.3.7). В итоге получим векторную задачу нелинейного программирования:
opt F (X) = { max f 1(X) = (p- 400) x 1 + (p- 400) x 2, (5.3.18)
min f 2(X) = px 1 + px 2}, (5.3.19)
при ограничениях
1468.33£ 2.60 p + x 1+ x 2 £ 1794.6, (5.3.20)
-622.67 £ -2.11 p + x 1+ x 2 £ -509.67, (5.3.21)
100000 ≤ px 1+p x 2 ≤ 300000,
400 x 1≤ 150000, 400 x 2≤ 150000, (5.3.22)
400£ p £ 800, x 1, x 2³ 0, (5.3.23)
где X= { p, x 1, x 2} – вектор неизвестных, определяющий цену и конструктивные параметры рыночного спроса – потребления;
(5.3.18)-(5.3.19)– функции, определяющие цели индивидуального производителя и индивидуального потребителя;
(5.3.20) – функция спроса, в ней bd- 10% bd= 1631.47-10%*1631.47=1468.33, bd+ 10% bd= 1794.6;
(5.3.21) – функция предложения: bs- 10% bs =-566.07-10%(-566.07)=-622.67, bs+ 10% bs =-509.47.
(5.3.22) - ограничения по бюджету потребителей и производственным мощностям производителей;
(5.3.23) – ограничения, накладываемые на цену и на не отрицательность объемов произведенной и проданной продукции.
Моделирование развития рынка (в нашем примере исследование) выполним путем решения двух вариантов векторной задачи (5.3.18)-(5.3.23) с различными ограничениями: функции спроса-предложения представлены равенствами, неравенствами (5.3.20)-(5.3.23).
Результаты решения проиллюстрируем на рис. 5.3 и 5.4.
1 вариант. Решение равенств (5.3.17), т. е. определения точки равновесия спроса и предложения, представим в системе Matlab.
[ q, c ] =solve ('q+ 2.60 *p= 1631.47', 'q- 2.11 *p =-566.07'). (5.3.24)
В результате решения получим: Xd=s= { p= 466.569, q = 418.39}. Эта точка представлена на рис. 5.4 в центре.
2 вариант. Для решения векторной задачи (5.3.18)-(5.3.23) используем метод, основанный на нормализации критериев и принципе гарантированного результата, на каждом шаге которого применяется алгоритм решения однокритериальной задачи нелинейного программирования, представленный в системе Matlab (функция fmincon (…)).
Шаг 1, 2. Решается задача (5.3.18)-(5.3.23) по каждому критерию отдельно – ищется наилучшее X  , k=
, k=  (К =2) и наихудшее решение X
(К =2) и наихудшее решение X  , k=
, k=  .
.
В результате решения получим:
X  ={ p =513.2, x 1=230.11, x 2=230.11}, f
={ p =513.2, x 1=230.11, x 2=230.11}, f  = f 1(X
= f 1(X  )=-52107,
)=-52107,
X 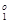 ={ p =419.9, x 1=188.2, x 2=188.2}, f
={ p =419.9, x 1=188.2, x 2=188.2}, f 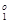 = f 1(X
= f 1(X 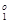 )=7512;
)=7512;
X  ={ p =443.9, x 1=157.03, x 2=157.03}, f
={ p =443.9, x 1=157.03, x 2=157.03}, f  = f 2(X
= f 2(X  )=139430,
)=139430,
X 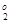 ={ p =489.2, x 1=261.3, x 2=261.3}, f
={ p =489.2, x 1=261.3, x 2=261.3}, f 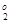 = f 2(X
= f 2(X 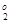 )=255670.
)=255670.
Эти точки представим на рис. 5.4 точками с соответствующими координатами: X 1 max ={ p =513.2, d =460.22}, X 1 min ={ p =419.9, d =376.4}, X 2 min ={ p =443.9, d =314.06}, X 2 max ={ p =489.2, d =522.6}, где с – стоимость товара, d = x 1+ x 2 - объем спроса-предложения. Область, ограниченная этими точками представляет собой область спроса-предложения.

Рис. 5.3. Функции спроса-предложения и результаты решения задачи
Результаты решения X  , X
, X  получены при условии, что каждому участнику рынка (производителю и потребителю) предоставляются наиболее благоприятные условия, т. е. при оптимизации учитываются только ограничения, накладываемые на их производственную деятельность и финансовые возможности. Практически показатели X
получены при условии, что каждому участнику рынка (производителю и потребителю) предоставляются наиболее благоприятные условия, т. е. при оптимизации учитываются только ограничения, накладываемые на их производственную деятельность и финансовые возможности. Практически показатели X  , f
, f  - это монополия для производителя, а X
- это монополия для производителя, а X  , f
, f  - монопсония для потребителя. Эти смоделированные показатели берем за цели, к которым стремится каждый участник рынка.
- монопсония для потребителя. Эти смоделированные показатели берем за цели, к которым стремится каждый участник рынка.
Шаг 3. Выполняется стандартная нормализация критериев и анализ результатов решения, полученных по каждому критерию.
fk (X  ) =
) =  ,
,
l k ( ) =
) =  .
.
На этом этапе цели каждого участника р f  , f
, f  по числовой величине выравниваются, в результате получим нормализованные цели l
по числовой величине выравниваются, в результате получим нормализованные цели l  = l k(X
= l k(X  )= 1, " k Î К, к которым должен стремиться каждый участник рынка.
)= 1, " k Î К, к которым должен стремиться каждый участник рынка.
Шаг 4. Построение и решение l-задачи:
l o= max l, (5.3.25)
l -  £ 0, (5.3.26)
£ 0, (5.3.26)
l -  £ 0, (5.3.27)
£ 0, (5.3.27)
1468.33£ 2.60 p +x 1 +x 2£ 1794.6, (5.3.28)
- 622.67 £ -2.11 p+x 1 +x 2 £ -509.67, (5.3.29)
100000≤ px 1+ px 2 ≤ 300000, 400 x 1≤ 150000, 400 x 2≤ 150000, x 1, x 2³ 0,

Рис. 5.4. Целевые функции производителя и потребителя на области спроса-предложения
В l-задаче целенаправленность определяется нижним уровнем l =min (l k (X), k=  ), " X Î S. l рассчитывается для всех критериев - как для производителей, так и для потребителей измеренных в относительных единицах, и в l-задаче этот уровень устремляется к максимуму, который в итоге равен lo.
), " X Î S. l рассчитывается для всех критериев - как для производителей, так и для потребителей измеренных в относительных единицах, и в l-задаче этот уровень устремляется к максимуму, который в итоге равен lo.
В результате решения l-задачи получаем точку оптимума Xo= { p= 477.9, x 1=202.2, x 2=202.2} см. рис. 5.3 и 5.4 и максимальную относительную оценку lo=0.5373 см. рис. 5.4, которая является максимальным нижним уровнем для всех относительных оценок lo=min (l k (Xo), k= 1, 2), т. е. гарантированным результатом в относительных единицах, который гарантирует, что в полученной оптимальной точке Xo все критерии равны или лучше lo, т. е. выполняются условия l k (Xo)³ l o, k =1, 2 или в общем виде: l o ≤ l k (Xo), k=  .
.
Действительно: f 1(Xo)=31488, f 2(Xo)=193210. l1(Xo) = 0.5376, l2(Xo)=0.5373.
Покажем функции, определяющие цели индивидуального производителя (5.3.8) и потребителя (5.3.9) на рис. 5.4.
Область спроса-предложения X1maxX2minX1minX2max, рассмотренная на рис. 5.4, представлена четырехугольником, который искусственно опущен до l= -1. Точка Xo , принадлежащая области спроса-предложения, является «седловой», в ней, во-первых, спрос равен предложению l1(Xo)=l2(Xo)=0.5373, во-вторых, это равенство максимальное.
В терминах стоимостей финансовые затраты производителей и потребителей также равны между собой:
få q (X) = 
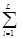 (pq +aql) xql=få l (X) =
(pq +aql) xql=få l (X) = 
 pqxql, (5.3.30)
pqxql, (5.3.30)
т.е. предложение равно спросу.
Заключение. Таким образом, в рассмотренной оптимизационной модели рынка (5.3.1)-(5.3.5) и его числового варианта (5.3.9)-(5.3.11) полученный результат – (равновесная цена и объем спроса – предложения) учитывает, во-первых, бюджет потребителя и возможности производителя, во-вторых, лежит в области, определяемой функциями спроса - предложения.