Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение модели рынка олигополии
|
|
Построение числовой модели олигополии, основные характеристики и параметры которой представлены выше, покажем на модели (5.4.6)-(5.4.10). Для олигополии характерно то, что стоимость продаж, затраты на производство продукции (производственно-экономические параметры) отличаются по величине. Эти требования отразим в математической модели рынка.
Дано. Введем обозначения, уточняющие модель (5.4.6)-(5.4.10):
c 1 = c 2 = 50, c 3 =c 4=60 - цены на продукт; a 1 = a 2 = 40, a 3 =a 4 = 50 - затраты;
p 1 =, …, =p 4 = (cj-aj )=10 - прибыль от производства и продажи продукта;
b 
= 3500, b 
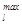= 5000, l= 1, 2; bq= 5000, q= 1, 2.
Взаимосвязь спроса и предложения решена аналогично, как и для модели совершенной конкуренции, т. е. в модели (5.4.6)-(5.4.10) с предлагаемыми числовыми параметрами, предложение превышает спрос, хотя модель может быть использована и при других взаимоотношениях спроса и предложения.
Построить оптимизационную модель рынка и рассчитать объемы спроса-предложения.
Построение математической модели рынка. Модель рынка с двумя производителями и двумя потребителями (модель 2*2) введенными параметрами в виде векторной задачи линейного программирования представим следующим образом:
opt F (X)={ max f 1(X) =10 x 1 +10 x 2, max f 2(X)= 10 x 3+10 x 4, (5.4.21)
min f 3 (X) = 50 x 1 + 60 x 3 , min f 4(X) = 50 x 2+ 60 x 4}, (5.4.22)
при ограничениях
3500 ≤ 50 x 1+60 x 3 ≤ 5000, 3500 ≤ 50 x 2+60 x 4 ≤ 5000, (5.4.23)
40 x 1+ 40 x 2 ≤ 5000, 50 x 3+ 50 x 4 ≤ 5000, (5.4.24)
x 1, x 2, x 3, x 4 ³ 0. (5.4.25)
Решение векторной задачи (5.4.21)-(5.4.25) на основе нормализации критериев и принципе гарантированного результата представим в виде последовательности шагов.
Шаг 1, 2. Решаем задачу (5.4.21)-(5.4.25) по каждому критерию отдельно. Ищется наилучшее (X 
), и наихудшее решение (X 
), т.е. для " k Î K 1= Q определяется максимум и минимум, а для " k Î K 2= L ищется минимум и максимум соответственно. В результате решения получим:
Критерий 1. max: X 
={ x 1=62.5, x 2=62.5, x 3=31.25, x 4=31.25},
f 1(X ) =1250.0, f 2(X ) =625.0, f 3(X ) =5000.0, f 4(X ) = 5000.0,
min: X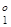 
={ x 1= 20.0, x 2= 0.0, x 3= 41.667, x 4=58.33},
f 1(X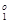 
)=200.0, f 2(X 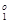)=1000.0, f 3(X 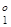)=3500.0, f 4(X 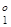)=3500.0.
Критерий 2. max: X 
={ x 1=40.0, x 2= 40.0, x 3= 50.0, x 4= 50.0},
f 1(X )=800.0, f 2(X )=1000.0, f 3(X )=5000.0, f 4(X )=5000.0,
min: X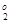 
={ x 1= 55.0, x 2=70.0, x 3= 12.5, x 4= 0.0},
f 1(X 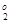)=1250, f 2(X 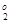) = 125, f 3(X 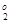) = 3500, f 4(X 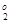) =3500.
Критерий 3. min: X 
={ x 1=33.6, x 2=45.9, x 3=30.33, x 4= 45.1},
f 1(X )= 795, f 2(X ) = 754, f 3(X )=3500, f 4(X ) = 5000,
max: X 
={ x 1=45.902, x 2=45.902, x 3=45.082, x 4= 45.082}.
f 1(X ) = 918, f 2(X ) = 901.64, f 3(X ) = 5000, f 4(X ) =5000.
Критерий 4. min: X 
={ x 1=45.9, x 2=15.9, x 3=45.08, x 4=45.1}.
f 1(X )= 618, f 2(X )=901.64, f 3(X )=5000, f 4(X ) =3500.
max: X 
={ x 1= 45.9, x 2= 45.9, x 3=45.082, x4 = 45.082}.
f 1(X )= 918, f 2(X )= 901.64, f 3(X )=5000, f 4(X ) =5000.
Шаг 3. Выполняем стандартную нормализацию критериев и проводим анализ оптимальных результатов решения, полученных по каждому критерию:
f 1(X )= 1250.0 f 2(X )=621.5 f 3(X )=4989.6 f 4(X )=4989.6
f 1(X )=677.1 f 2(X )=1000.0 f 3(X )=4692.7 f 4(X )=4692.7
f 1(X )=808.1 f 2(X )=688.8 f 3(X )=3500.0 f 4(X )=4673.0
f 1(X )=808.1 f 2(X )=688.8 f 3(X )=4673.0 f 4(X )=3500.0
l1(X )=1.0, l2(X )=0.5675, l3(X )=0.0, l4(X )=0.0,
l1(X )=0.4543, l2(X )=1.0, l3(X )=0.2, l4(X )=0.2,
l1(X )=0.579, l2(X )=0.644, l3(X )=1.0, l4(X )=0.2,
l1(X )=0.579, l2(X )=0.644, l3(X )=0.2, l4(X )=1.0.
Шаг 4. Построение и решение l-задачи. Она примет вид:
l o = max l, (5.4.26)
при ограничениях
l - (p 1 x 1 + p 2 x 2 - f 1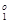(X ))/(f 1(X ) -f 1(X 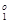))£ 0, (5.4.27)
l - (p 3 x 3 + p 4 x 4 - f 2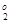(X ))/(f 2(X ) -f 2(X 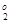))£ 0,
l - (c 1 x 1 + c 3 x 3- f 3(X ))/(f 3(X ) -f 3(X ))£ 0,
l - (c 2 x 2 + c 4 x 4 - f 4(X ))/(f 4(X ) -f 4(X ))£ 0, (5.4.28)
3500 ≤ c 1 x 1 + c 3 x 3 ≤ 5000, 3500 ≤ c 2 x 2 +c 4 x 4 ≤ 5000, (5.4.29)
a 1 x 1 +a 2 x 2 ≤ 5000, a 3 x 3 +a 4 x 4 ≤ 5000, x 1, x 2, x 3, x 4 ³ 0. (5.4.30)
Решение l-задачи.
В результате решения l-задачи получаем точку оптимума Xo, fk (Xo), k= 
и максимальную относительную оценку l o:
l o = 0.61112, Xo ={ x 1=42.1, x 2= 42.085, x 3=32.986, x 4= 32.98}.
f 1(Xo) = 841.6, f 2(Xo) =659.7, f 3(Xo) = 4083.3, f 4(Xo) = 4083.3,
l1(Xo)=0.61112, l2(X0)=0.61112, l3(Xo)=0.61112, l1(Xo) =0.61112,
т. е. выполняются условия l o ≤ l q (Xo), q= 1, 2, 3, 4. Любое улучшение (увеличение) одного из них приводит к ухудшению другого.