Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дальше не надо
|
|
Пример 1. Линейная модель рынка.
Методологию моделирования рынка проведем в три этапа: постановка задачи, построение модели вида (5.3.1)-(5.3.5) и непосредственно моделирование.
Постановка задачи.
Дано. На объем производства и соответственно продаж оказывают влияние:
· производственные возможности производителей: a 1 =a 2=400 - затраты на производство продукта у обоих производителей, b 1 =b 2=150000 - финансовые возможности фирм при производстве продукта;
· цены на выпускаемый продукт фиксированы cq =500, q =1, 2;
· финансовые возможности (бюджетные ограничения) потребителей: b 
=100000, b 
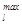=300000, " lÎ L – минимальный и максимальный объем финансовых средств, в рамках которого они может осуществлять покупки продукта от разных фирм. Максимальная цена, которую в состоянии оплатить потребители, cmax =800.
Построить математическую модель рынка на основе оптимизационной задачи (5.3.1)-(5.3.5) и решить ее.
Построение модели рынка. Обозначим: x1, x2 – вектор переменных, характеризующий объемы продукции, произведенные первым и вторым производителем соответственно. Так как цены на выпускаемый продукт фиксированы, то это позволяет рассматривать задачу (5.3.1)-(5.3.5) как линейную.
С учетом введенных обозначений математическая модель рынка (5.3.1)-(5.3.5) может быть представлена в виде векторной задачи линейного програм мирования:
opt F (X) = { max f 1(X) = p 1 x 1 + p 2 x 2 ,
min f 2(X) = p 1 x 1 + p 2 x 2},
при ограничениях b 
≤ p 1 x 1 + p 2 x 2 ≤ b 
, a 1 x 1 ≤ b 1, a 2 x 2 ≤ b 2, x 1, x 2³ 0,
или в числовом виде: pq =500, aq =400, p q=pq - aq =100, bq =150000, q =1, 2, b =100000, b =300000
opt F (X)={ max f 1(X) = 100 x 1 + 100 x 2 ,
min f 2(X) = 500 x 1 + 500 x 2 , (5.3.9)
при ограничениях 100000≤ 500 x 1+500 x 2≤ 300000, (5.3.10)
400 x 1≤ 150000, 400 x 2≤ 150000, x 1, x 2 ³ 0. (5.3.11)
где (5.3.9) - критерии производителей, максимизирующих свои прибыли; и критерии потребителей, минимизирующие свои затраты; (5.3.10) - ограничения по финансовым возможностям потребителя при приобретении первого и второго товара; (5.3.11) – ограничения по производственным мощностям при производстве двух товаров.
Для решения векторной задачи (5.3.9)-(5.3.11) использован алгоритм, основанный на нормализации критериев и принципе гарантированного результата при равнозначных критериях. На каждом шаге алгоритма используется симплексный алгоритм, представленный в системе Matlab.
Шаг 1, 2. Решается задача (5.3.9)-(5.3.11) по каждому критерию отдельно (наилучшее, наихудшее). В результате решения получим:
X 
={ x 1=300, x 2=300}, f = f 1(X )=60000,
X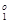 
={ x 1=100, x 2=100}, f 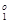= f 1(X 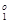)=20000;
X 
={ x 1=100, x 2=100}, f = f 2(X )=100000,
X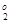 
={ x 1=300, x 2=300}, f 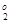= f 2(X 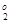)=300000.
Шаг 3. Выполняется стандартная нормализация критериев и анализ результатов решения, полученных по каждому критерию.
fk (X ) =[ f 1(X )=60000, f 2(X )=300000;
f 1(X )=20000, f 2(X )=100000].
l k (X ) =[l1(X )=1.0, l2(X )=0.0; l1(X )=0.0, l2(X )=1.0].
Шаг 5. Построение l-задачи:
lo= max l, (5.3.12)
l - 
£ 0, (5.3.13)
l - 
£ 0, (5.3.14)
100000≤ 500 x 1+500 x 2 ≤ 300000, (5.3.15)
400 x 1≤ 150000, 400 x 2≤ 150000, x 1, x 2³ 0. (5.3.16)
Шаг 4. Решение l-задачи (5.3.12)-(5.3.16). lo = 0.5,
Xo ={ x 1=0.4999, x 2=373.73, x 3=26.31}. f 1(Xo)=40000, f 2(Xo)=200020. l1(Xo)=0.4999, l2(X0)=0.5001, т. е. выполняются условия l o ≤ lk(Xo), k =1, 2.
В терминах стоимостей финансовые затраты производителей и потребителей равны между собой:
få q (X) =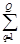 
(pql+aql) x 
=få l (X) = 
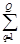pqxql,
- предложение равно спросу.