
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Моделирование поведения отдельного производителя с учетом статистической функции предложения
|
|
Для построения модели поведения отдельного производителя на какой-либо период с учетом статистических данных используем результаты эконометрического анализа функции предложения q-го производителя. Рассмотрим линейную функцию предложения [3]:
q  = b o ' + b xpх +b wpw +b rpr +b hhx, (5.2.25)
= b o ' + b xpх +b wpw +b rpr +b hhx, (5.2.25)
где q  (s - supply - предложение) - количество требуемого товара X, pх - цена этого товара, pw - цена исходных ресурсов, необходимых для производства (например, цена на сырьё, заработную плату основных производственных рабочих и т. д.), pr - цена технологически однородных товаров, hx - значение любой другой переменной, влияющей на предложение товара на рынке, (например, доступность технологий, число конкурентов на рынке, размер налогов или ожидания производителей);
(s - supply - предложение) - количество требуемого товара X, pх - цена этого товара, pw - цена исходных ресурсов, необходимых для производства (например, цена на сырьё, заработную плату основных производственных рабочих и т. д.), pr - цена технологически однородных товаров, hx - значение любой другой переменной, влияющей на предложение товара на рынке, (например, доступность технологий, число конкурентов на рынке, размер налогов или ожидания производителей);
b o ', b x, b w, b r, b h – это фиксированные коэффициенты, величины которых могут быть получены на основе исследования статистических данных реализации товара, используя регрессионный анализ.
Преобразуем это выражение, предполагая, что факторы сw, pr, hx не изменяются, а q  =
=  xql (t), " q Î Q, в итоге из (5.2.25) получим:
xql (t), " q Î Q, в итоге из (5.2.25) получим:
 xql (t)=b o ''+b xpх, " q Î Q,
xql (t)=b o ''+b xpх, " q Î Q,
где b o ''=b o ' +b wpw +b rp r +b hhx.
Вычислим из этого выражения цену товара:
pх = b o + b l  xql (t), " q Î Q,
xql (t), " q Î Q,
где b o =(b o ' +b wpw +b rpr +b hhx)/b x, b l =1/b x.
Перенесем в этом уравнении все (L+1) переменные в левую часть и приведем равенство к стандартному виду:
p -  al xql (t)= bs, " q Î Q, (5.2.26)
al xql (t)= bs, " q Î Q, (5.2.26)
где p = pх, al=bl, bs = b o.
Цель любого производителя продать как можно больше товара по наиболее возможно высокой цене, с тем, чтобы получить, возможно, высокую прибыль. Эту целенаправленность можно представить в виде задачи математического программирования (ЗМП):
" q Î Q max fq (X (t))=  p qxql (t), (5.2.27)
p qxql (t), (5.2.27)
при ограничениях
p -  al xql (t)= bs, (5.2.28)
al xql (t)= bs, (5.2.28)
 aqxql (t)£ bq, aq £ p £ pmax, xql (t)³ 0. (5.2.29)
aqxql (t)£ bq, aq £ p £ pmax, xql (t)³ 0. (5.2.29)
где fq (X (t)) - целевая функция (критерий), управляющие переменные p q = pq - aq и xql, " q Î Q представлены в задаче произведением, а отсюда задача оптимизации (5.2.27)-(5.2.29) – не линейна, в ней производитель максимизирует свои прибыли за счет изменения стоимости; (5.2.28) - ограничения по предложению на данном рынке (функция предложения); (5.2.29) - ограничения по ресурсным возможностям q -го производителя.
Задача (5.2.27)-(5.2.29) является моделью поведения любого q Î Q производителя на дискретный период t Î T.
Методологию построения модели и моделирования покажем на примере решения оптимизационной задачи (5.2.27)-(5.2.29).
Пример 7.3. (Нелинейная модель производителя с функцией предложения).
Дано. Статистические данные о цене и производстве (с последующей продажей) телевизоров. Они получены путем опроса десяти производителей телевизионных приемников на предмет объема производства при заданной цене. Объем производства приемников будем считать величиной переменной, а цену – исходной. Вид статистических данных представлен в табл. 5.2.
Таблица 5.2
Статистические данные о цене и количестве произведенных телевизоров
| Наблюдение | ||||||||||
| Количество (Var 1) | ||||||||||
| Цена (Var 2) |
Рассматривается две фирмы, выпускающие один продукт. Обозначим: x 1, x 2 – вектор переменных, характеризующий объемы продукции, произведенные первым и вторым производителем соответственно. На объем производства и соответственно продажи оказывают влияние производственные возможности фирм: a 1, a 2 - затраты на производство продукта у обоих производителей; bq, q =1, 2, - финансовые возможности фирм при производстве продукта; b  , b
, b  - минимальный и максимальный объем финансовых средств, которые могут выделить на покупку продукта от разных фирм потребитель; x
- минимальный и максимальный объем финансовых средств, которые могут выделить на покупку продукта от разных фирм потребитель; x  - минимальный объем товара, которые потребляет от разных фирм потребитель.
- минимальный объем товара, которые потребляет от разных фирм потребитель.
Примем: a 1= a 2=400, b 1= b 2=150000, b  =100000, b
=100000, b  =300000.
=300000.
Требуется провести регрессионный анализ статистических данных, т. е. построить линию регрессии и определить статистические параметры регрессии, построить функцию предложения, оптимизационную модель предложения с использованием этой функции и рассчитать оптимальную цену и объемы производства обоих производителей.
Решение проведем в три этапа: используя, статистические данные табл. 5.2. построим функцию предложения, на ее основе построим оптимизационную модель, которая ее учитывает, и проведем расчет оптимальной цены и объемов производства.
Построим функцию предложения, для чего проведем регрессионный анализ статистических данных табл. 5.2. Введем статистические данные табл. 5.2 в электронные таблицы программы Statistica (Система программного обеспечения анализа данных) [8] и поведем расчет. В результате расчета получим: средние значения цены и реализуемого товара, а также данные регрессионного анализа.
Таким образом, линейной функцией предложения на телевизоры, при которой минимизируется квадрат погрешностей между множеством фактических точек и линией, произведенной через это множество, является уравнение:
q  = -566, 07 + 2, 11 pх. (5.2.30)
= -566, 07 + 2, 11 pх. (5.2.30)
Это уравнение и соответствующие параметры регрессионного анализа показаны на рис. 5.3.
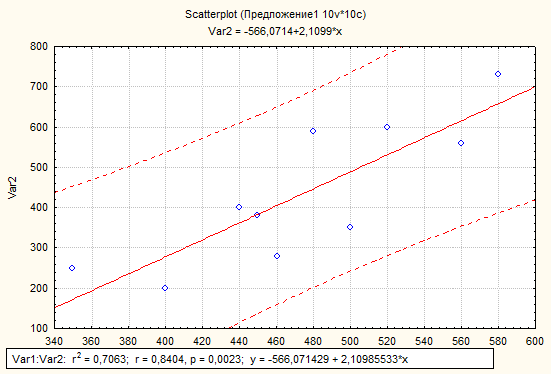
Рис. 5.3. Функция предложения и параметры регрессионного анализа
Построим оптимизационную задачу с учетом функции предложения.
Функция предложения представлена уравнением: q  = -566, 07 + 2.11 pх, которое приведем к виду:
= -566, 07 + 2.11 pх, которое приведем к виду:
x 1 + x 2 - 2.11p= -566.07, (5.2.31)
где p = pх определяет величину рыночной стоимости на товар – телевизоры, при совокупном объеме производства: q  = x 1 + x 2 .
= x 1 + x 2 .
Используя (5.2.31) построим задачу нелинейного программирования:
max f (X) = (p -400) x 1 + (p -400) x 2 , (5.2.32)
при ограничениях x 1 + x 2 - 2.11 p = -566.07, (5.2.33)
100000≤ px 1 + px 2 ≤ 300000, (5.2.34)
400 x 1≤ 150000, 400 x 2≤ 150000, x 1, x 2, с ³ 0, (5.2.35)
где X ={ x 1, x 2, p } – вектор неизвестных, определяющий конструктивные параметры рыночного предложения индивидуального производителя.
Решим задачи нелинейного программирования (5.2.32)-(5.2.35), используя алгоритм, представленный в системе Matlab (функция fmincon (…)) [39]. В результате решения получим: X *={ x 1=357.8, x 2=203.6, p =534.4}, f *=75431.
Максимальный уровень производства фирмы определяется кривой предложения:
x 1 + x 2 -2.11 p = 357.7785+ 203.6442 -2.11*534.3567=-566.07.
Результаты: q  = x 1 + x 2 =561.4 и p =534.4 представляют координаты точки функции спроса на рис. 5.3.
= x 1 + x 2 =561.4 и p =534.4 представляют координаты точки функции спроса на рис. 5.3.
Если решать задачу минимизации - min f (X), то в результате решения получим: X *={ x 1=128.25, x 2=128.25, p =389.8483}, f* =2604.0, при этом x 1 + x 2 -2.11 p = 128.25+ 128.25+2.11*389.85=-566.07, т. е. результат также удовлетворяет кривой предложения.
Таким образом, в рассмотренной оптимизационной модели индивидуального производителя (5.2.32)-(5.2.35) полученный результат учитывает, с одной стороны, мощности производителя, а с другой соответствие функции предложения.