
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Признаки сходимости неотрицательных рядов (предельный приз; приз сравнения).
|
|
Числовые ряды. Св-ва сходящихся рядов. Необходимый приз сх-ти ряда
Пусть дана пос-ть чисел: 
Опр: Числовым рядом наз-ся выражение 

Гармонический ряд.
Обозначим S1=a1; S2=a1+a2;
 n ая сумма ряда
n ая сумма ряда
Опр: Ряд (1) наз-ся сходящимся если сущ-ет конечный 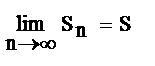 ;
;  .
.
Если конечного предела  не сущ-ет, то ряд наз-ся расходящимся.
не сущ-ет, то ряд наз-ся расходящимся.
 .Геомет-ий ряд.
.Геомет-ий ряд.  .
.
1) если  ,
,  при
при 
 , ряд сходящихся.
, ряд сходящихся.
2) если 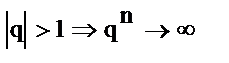
 ряд расходящихся.
ряд расходящихся.
3) если  ряд а+а+а+…+а+…
ряд а+а+а+…+а+…

4) если q=-а+а-а+а-а…
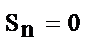 , если n – четное
, если n – четное
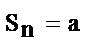 , если n – нечетное
, если n – нечетное
 - не сущ-ет. Ряд рас-ся.
- не сущ-ет. Ряд рас-ся.
Св-ва сходящихся рядов:
1) если  сх-ся к сумме S. То
сх-ся к сумме S. То 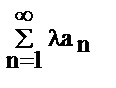 сх-ся к сумме
сх-ся к сумме  .
.
2) если  и
и 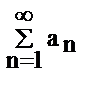 сх-ся, то ряд
сх-ся, то ряд  сх-ся.
сх-ся.
3) если  сх-ся, то сх-ся ряд, полученный из исходного отбрасывания конечного числа слагаемых.
сх-ся, то сх-ся ряд, полученный из исходного отбрасывания конечного числа слагаемых.
Необходимый признак сх-ти ряда.
Если ряд  сх-ся, то
сх-ся, то 
Д-во:
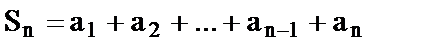

По усл. ряд сход-ся т.е.  конечный
конечный 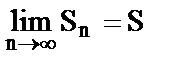


Следствие:  , то ряд рас-ся.
, то ряд рас-ся.
Зам:  рас-ся ряды, для кот
рас-ся ряды, для кот 
Признаки сходимости неотрицательных рядов (предельный приз; приз сравнения).
Теорема 1 (признак сравнения)
Даны два знакоположительных ряда  и
и  ,
, 
Тогда: 1) если  сх-ся, то сх-ся ряд
сх-ся, то сх-ся ряд 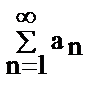 2) если
2) если  рас-ся, то рас-ся ряд
рас-ся, то рас-ся ряд 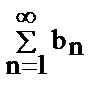
Док-во: Обозначим  - частичная сумма
- частичная сумма  ,
,  -
-  .Т.к..
.Т.к..  , то
, то 
1) если  сх-ся к сумме
сх-ся к сумме  , то посл.
, то посл.  ограничена, по лемме
ограничена, по лемме 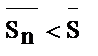

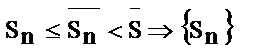 ограничена
ограничена  по лемме
по лемме  сх-ся
сх-ся
2) 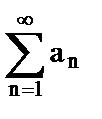 рас-ся, тогда
рас-ся, тогда  возрастает
возрастает 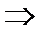

 рас-ся.
рас-ся.
Теорема 2 (предельный признак сравнения) Пусть для знакоположительных рядов  ,
,  выполнено
выполнено  . Тогда ряды ведут себя одинаково
. Тогда ряды ведут себя одинаково