
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Производная неявно заданной функции.
|
|
Теорема.: Пусть непрерывная ф-я y от x задается ур-ем F(x, y)=0, где F(x, y), Fx’(x, y), Fy’(x, y) – непрерывные ф-и в области D, Fy’(x, y)≠ 0. Тогда y’x=  .
.
Док-во: F(x, y)=0,  F(x+∆ x, y+∆ y)=0
F(x+∆ x, y+∆ y)=0
F(x+∆ x, y+∆ y)- F(x, y)=0 – это полное приращение к ф-и F(x, y).
 , где γ 1, γ 2→ 0 при ∆ x, ∆ y→ 0
, где γ 1, γ 2→ 0 при ∆ x, ∆ y→ 0
 ;
; 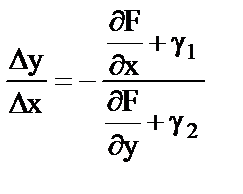 ;
;  ;
;
Рассмотрим случай трех переменных. Ур-е вида F(x, y, z)=0 задает ф-ю z =z(x, y) неявно.
Найдем частные производные z’x, z’y
z’x=  ; z’y=
; z’y=  ;
;
Производная по направлению.
| y |
| x |
| y0 |
| y0+∆ y |
| x0+∆ x |
| x0 |
| (x0+∆ x, y0+∆ y) |

|
| P0 |
Определить в данной точке P0 скорость изменения ф-и в заданном направлении.
∆ x = ∆ l cosα
∆ y = ∆ l sinα
∆ u=f(x0+∆ x, y0+∆ y)-f(x, y)= 
Делим на ∆ l:  Опр.: Производной ф-и u=f(x, y) по направлению вектора
Опр.: Производной ф-и u=f(x, y) по направлению вектора  наз-ся
наз-ся 

 ;
;  , где β – угол между
, где β – угол между  и Оy;
и Оy;
Зам: 1)  скорость изменения u по оси Ox;
скорость изменения u по оси Ox;
 скорость изменения u по оси Oy;
скорость изменения u по оси Oy;
2) Если u = u(x, y, z), то
 .
.