
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Радиус сходимости. Св-ва степенных рядов. Разложение ф-й в степенные ряды.
|
|
Опр: Пусть R действительное неотрицательное число:  при
при 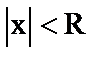 ряд
ряд  сх-ся, при
сх-ся, при  ряд рас-ся. R – радиус сходимости степенного ряда. Если ряд сх-ся только в т.х=0, то R=0.
ряд рас-ся. R – радиус сходимости степенного ряда. Если ряд сх-ся только в т.х=0, то R=0.
Опр: Совокупность всех x, при которых степенной ряд сх-ся наз-ся интервалом сходимости  .
.
Опр: Областью сходимости наз-ся интервал  , к которому в зависимости от конкретных случаев могут быть добавлены концевые точки -R или R.
, к которому в зависимости от конкретных случаев могут быть добавлены концевые точки -R или R.
Св-ва степенных рядов.
1) Пусть степенной ряд  имеет интервал сходимости
имеет интервал сходимости 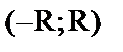 тогда он равномерно сх-ся на
тогда он равномерно сх-ся на  где
где  .
.
2) Сумма степенного ряда 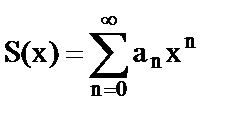 явл-ся непрерывной ф-ей в каждой т. обл. сх-ти.
явл-ся непрерывной ф-ей в каждой т. обл. сх-ти.
3) Степенной ряд можно дифференцировать в каждой т. интервала сходимости. Полученный ряд имеет тот же интервал сходимости.
4) Степенной ряд можно интегрировать  где
где  интегралу сх-и.
интегралу сх-и.
Разложение функций в степенные ряды:
1) Ф-я  непосредственно раскладывается в ряд Тейлора.
непосредственно раскладывается в ряд Тейлора.
2) Использование табличных разложений

 .
.


 .
.
3) Сложение, вычитание, умн. на ф-ю.
4) Использование дифференцирования и интегрирования рядов.
8. Периодические функции. Ортогональность тригонометрической системы.
Опр: Функция φ (t) наз-ся периодической с периодом Т≠ 0, если φ (t + T) = φ (t).
Опр: Система ненулевых ф-й φ 1(x), φ 2(x), … φ n(x)…={φ (x)} наз-ся ортогональной на [a, b], если  dx=0, n
dx=0, n  m.
m.
Опр: Система {φ n}={1, cosx, sinx, cos(2x), sin(2x), …, cos(nx), sin(nx), …} – наз-ся тригонометрической системой на  .
.
Покажем ортог-ть этой триг-ой системы, т.е.
 n
n  m
m
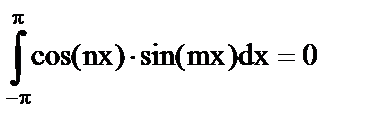 n
n  m
m

 n, m
n, m


Док-во:
 =
=
 =0
=0
2) n = m  (др. рав-ва док-ся аналогично)
(др. рав-ва док-ся аналогично)