Геометрические и физ. приложения кратных, криволинейных, поверхн. интегралов.

1. Если 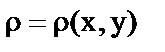плотность плоской пластины, то ее масса М= 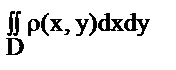, координаты ц.т.: 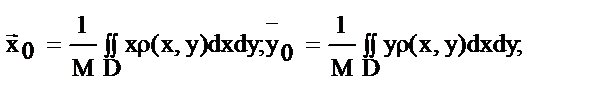2. Момент инерции пластины отн-но осей Оx, Oy:

;

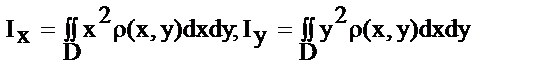3.Если 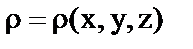плотность тела G, то его масса М= 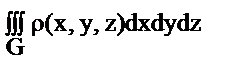, коор-ы ц.т.: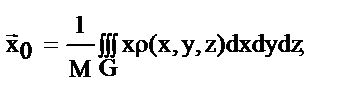

4. Момент инерции тела G отн-но пл-ей xy, yz, xz:

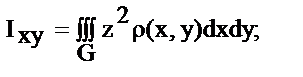
5. 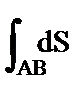-длина дуги АВ;

6. Если f(x, y) плотность, распределенной по дуге АВ, то 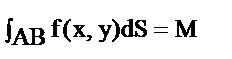-масса дуги АВ

7. 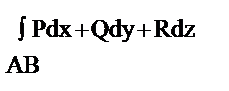-работа переменной силы 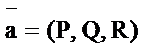вдоль дуги кривой АВ;

8. 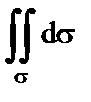-площадь поверхности ;

9. Если F(x, y, z) плотность, распределенная по поверхности , то 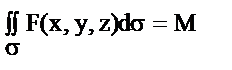-масса поверхности

10. 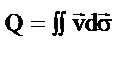кол-во жидкости, протекающей ч/з поверхность

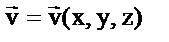- скорость

11. Корд. ц т однородной кривой К: 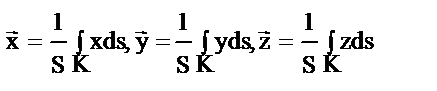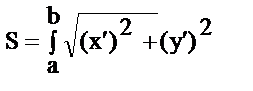- длина дуги

38. Обыкновен диф ур-я: опр, общ реш, част реш. Общ вид диф ур-я 1-го порядка. Задача Коши.

Опр: Диф ур-ем наз-ся ур-е, связывающее независимую первую х, искомую ф-ю y=f(x) и её произ-е

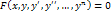(1)

Если искомая ф-я зависит только от 1ой переменной х, то дифференцирование наз-ся обыкновенным.

Если ф-я зависит от нескольких переменных, то диф ур-е наз-ся диф ур-м с частными произв-ми.

Опр: Наивысший порядок произвольной неизвестной ф-и, входящей в диф ур-е, наз-ся порядком этого диф ур-я.

Опр: Любая ф-я 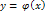, обращающаяся в ур-е (1) тож-во, наз-ся реш этого ур-я, а график ф-и наз-ся интегральной кривой.

Опр: Если реш. задано в неявном виде 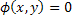, то оно обычно наз-ся интегралом ур-я (1).

Опр: Ф-я 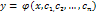, создающая n-независимых независимых произвольных const 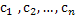, наз-ся общим реш. ур-я (1), если она яв-ся реш ур-я (1) при любых значениях констант.

Опр: Общий вид диф ур-я 1ого порядка 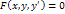(2) или 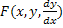, 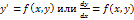Эти ур-я определяют наклон 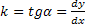интегральной кривой. k = f(x, y), если в некоторой обл. ф-я f(x, y) непр-а и имеет огр-ю производную 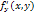, то через каждую внутреннюю т. 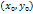пройдет единственная интегральная кривая. 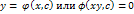или в этой обл. можно найти ф-ю, которая удовлетворяет усл-м при 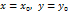, вып-ся.

Опр: Задача в кот. требуется найти частное решение ур-я y’=f(x, y), удовлетворяющим нач. усл. 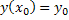, наз-ся зад. Коши.