Ряды Фурье для четных и нечетных периодических функций.

Если f(x)=f(-x) 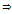f(x) – четная.

Если f(-x)=-f(x) 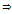f(x) – нечетная.

если- f(x) нечетная.

если f(x) – четная.

1) f(x) – периодическая на

= ⇒ =

= =

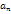Ряд Фурье

f(x)= + разложение по косинусам.

2) - нечетная ф-я

a₀=0;

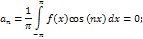
dx

Ряд фурье

Ряд Фурье для ф-й с произвольным периодом.

f(x)- периодическая ф-я, период T=2ℓ достаточно рассмотреть на [-ℓ; ℓ ]

x= , делаем замену переменной, t

Ф-и f(x) соответствует ф-я F(t)=f – период, T=2π.

Ряд Фурье для F(t)

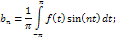
Т. o: f(x) , где

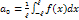
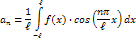
dx;

11. Ф-и многих переменных. Множества в Rⁿ : открытые, замкнутые, ограниченные.

Опр.: Если каждой паре (x, y) из некоторого мн-ва D ставится в соответствие опред-е значение z, то z=f(x, y) – функция двух независимых переменных (x, y), определенная в D.

Опр.: Совокупность значений (x, y), для которых функция определена, наз-ся областью определения.

Опр.: δ – окрестность т.(x₀, y₀) наз- ся все точки, лежащие в круге радиуса δ и с центром в т.(x₀, y₀).

Опр.: Т.(x₀, y₀) наз-ся внутренней для множества D, если она 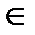D вместе с δ – окрестностью.

Опр.: Открытой областью наз-ся мн-во, если все точки этого мн-ва внутренние, и любые две точки мн-ва можно соединить непрерывной линией, лежащей в мн-ве.

Опр.: Т.(x₁, y₁) наз-ся граничной, если в окрестности этой точки есть точки и 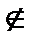мн-ву.

Опр.: Замкнутая обл = D {граница}.