Опр и св-ва крив-го интеграла 2-го рода. Формулы для вычисления.

Пусть на кривой АВ заданны ф-и P(x, y) и Q(x, y) x_k – проекция дуги A_k--1 A_kна ось Оx yk – проекция - - - - на ось Он составим суммы Y_k

Опр: 1)Криволинейный интеграл II рода по координате x наз-ся

2)По координате y -

3)Полный криволинейный интеграл II рода

Зам: =

Формулы для вычисления

1) y= - кривая АВ

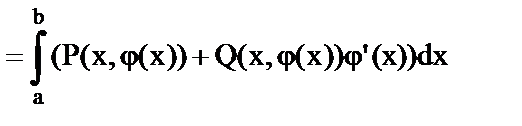
2) x= =

Независимость крив-го инт 2го рода от пути инт-я.Ф-ла Грина. Ф-ла для вычисления площади.

Утв. 2. Криволинейный интеграл 2 рода 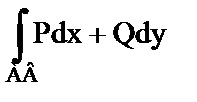не зависит от пути интегрирования, т.е. от формы кривой соединяющей т.А и В, если

Зам. Если С – замкнутый контур, то , если выполнено утверждение 2Теорема: Если D-замкнутая плоская область, ограниченная контуром Г, ф-и Р(х, у), Q(х, у) непрерывны в этой области вместе со своими частными производными , то имеет место рав-во (Формула Грина), где граница Г обходится против часовой стрелки.