Диф ур-я с разделяющимися переменными. Однор ур-я 1ого пор.

Ур-е 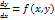dy – f(x, y)dx = 0. частный случай общ. ур-я.

Опр: Ур-е вида P(x)dx + Q(y)dy = 0 наз-ся диф ур-ем с разделяющимися переменными. Данное ур-е можно проинтегрировать .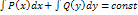

Опр: Ур-е вида 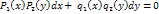наз-ся диф ур-ем с разделяющимися переменными. Это ур-е сводится к ур-ю с разделяющимися переменными путем деления на выражение P=(y)q₁(x): 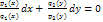можно интегрировать. Нужно иметь в виду, что при делении может произойти потеря реш, поэтому нужно проверять, явл. ли реш =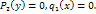

Опр: Ф-я F(x, y) наз-ся однородной ф-й порядка n отн-но переменных x, y если 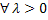вып-ся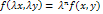

Опр: Ур-е вида 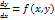наз-ся однородным отн-но переменных x, y, если правая часть f(x, y) – однородная ф-я нулевого порядка.

Замена: Y = xu(x) сводится к у-ю с разделяющимися переменными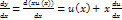

Т.к 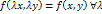Возьмем в кач-ве 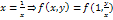т.е. f зависит от отн. 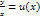. Подставим в ур-е .

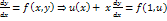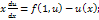xdu=f(1, u) – u(x)dx – ур-е с разделяющимися переменными.

Делим на x(f(1, u)-u): 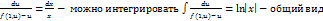находим u=u(x)=> y=xu(x)

Находите u=u(x)=> y=xu(x) – реш.