
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение и свойства двойного интеграла.
|
|
| y |
| x |
| Di |
число эл-ов Di: i=1, n. Δ Si – площадь каждого эл-та.
Опр. Наибольшее расстояние между точками, лежащими на
Границt области – диаметр области.
Опр. Наибольший диаметр эл-ов разбиения – мелкость разбиения.
Опр. σ (f)=  – интегральная сумма (Римана).
– интегральная сумма (Римана).
Опр. Пределы интегрирования сумм при мелкости разбиения, стрем. к нулю, наз-ся двойным интегралом от ф-и f по области D. ∫ ∫ f(x, y)dxdy.
Основные св-ва.
1. 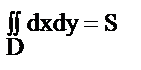 – площадь области D. Док-во:
– площадь области D. Док-во:  .
.
2.Линейность: для  f, g и const λ, μ вып-ся: ∫ ∫ (λ f(x, y)+μ g(x, y))dxdy= λ ∫ ∫ f(x, y)dxdy+ μ ∫ ∫ g(x, y)dxdy.
f, g и const λ, μ вып-ся: ∫ ∫ (λ f(x, y)+μ g(x, y))dxdy= λ ∫ ∫ f(x, y)dxdy+ μ ∫ ∫ g(x, y)dxdy.
Док-во:  3. Аддитивность. D=D1
3. Аддитивность. D=D1  D2.
D2. 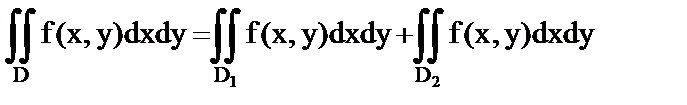 4.Монотонность для ф-ий f, g. При f(x, y)≤ g(x, y) ∫ ∫ f(x, y)dxdy≤ ∫ ∫ g(x, y)dxdy.
4.Монотонность для ф-ий f, g. При f(x, y)≤ g(x, y) ∫ ∫ f(x, y)dxdy≤ ∫ ∫ g(x, y)dxdy.
5.Оценка модуля: для  f(x, y) вып-ся
f(x, y) вып-ся 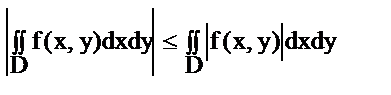
6.Св-во о среднем значении: для  f вып-ся нер-во
f вып-ся нер-во  (M – max значение ф-ии, S – площадь обл.)
(M – max значение ф-ии, S – площадь обл.)