
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
A. Параўнанні. Колца рэштаў. Абарачальныя элементы колца рэштаў.
|
|
Азн.1: Няхай n 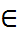 N, a, b
N, a, b 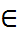 Z. Будзем казаць, што a параўнальны з b па модулі n, калі n дзеліць (a-b), г.зн. (a-b) дзеліцца на n. Запісваецца a
Z. Будзем казаць, што a параўнальны з b па модулі n, калі n дзеліць (a-b), г.зн. (a-b) дзеліцца на n. Запісваецца a  b(mod n).
b(mod n).
Уласцівасці парананняў:
 ;
;
2.  ;
;
3.  – дачыненне параўнальнасці па модулі n ёсць дачыненне эквівалентнасці на мностве Z;
– дачыненне параўнальнасці па модулі n ёсць дачыненне эквівалентнасці на мностве Z;

 ;
;

Сцв.1: Цэлыя лікі a, b 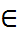 Z,
Z,  к.іт.к. яны маюць роўныя астачы пры дзяленні на n.
к.іт.к. яны маюць роўныя астачы пры дзяленні на n.
Доказ: Падзелім a і b з астачаю на n, г.зн. запішам іх у выглядзе: 
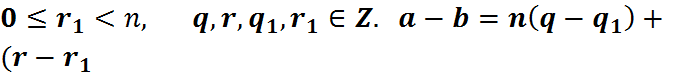 ) n дзеліцца на
) n дзеліцца на 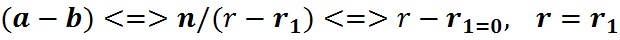 .
. 
З уласцівасці 3) вынікае, што Z падзяляецца на неперасякальныя класы параўнальных па модулі n лікаў. Паводле сцв.1 2 цэлыя лікі належаць аднаму класу к.іт.к. калі яны маюць аднолькавыя астачы пры дзяленні на n. Гэтыя класы наз. рэштамі па модулі n.
Вызначым на мностве  аперацыі складання і множання формуламі:
аперацыі складання і множання формуламі:


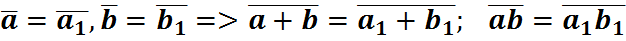 .
.
Тэарэма 2: Мноства  у дачыненні да аперацыяў (1) ёсць камутатыўнае колца з адзінкаю.
у дачыненні да аперацыяў (1) ёсць камутатыўнае колца з адзінкаю.
Колца  наз. колцам рэштаў па модулі n.
наз. колцам рэштаў па модулі n.
Тэарэма 2: 
 абарачальны ў
абарачальны ў  к.іт.к.
к.іт.к.  узаемна простыя.
узаемна простыя. 
Доказ:  абарачальны ў
абарачальны ў  к.іт.к.
к.іт.к.  абарачальны ў
абарачальны ў 
4. A. Ідэал колца. Азначэнне, прыклады, крытэр ідэалу. (5)