Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
B. Галоўны ідэал. Колцы галоўных ідэалаў.
|
|
Азн.2: Камутатыўнае колца з 1 ≠ 0, у якім кожны ідэал галоўны, наз. колцам галоўных ідэалаў.
Тэарэма 3: Колца цэлых лікаў Z ёсць колца галоўных ідэалаў.
Доказ: Няхай 
, нулявы ідэал (0) – галоўны, таму будзем лічыць, што 
, зн. 
. Разaм з a (-a 
), і таму ў I ёсць дадатны лік. Няхай b - мінімальны дадатны лік з I. Пакажам, што 
. 
, бо 
. 
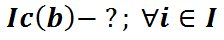падзелім на b з астачай 
З доказу вынікае, што адвольнае падколца колца Z ёсць галоўны ідэал Z.
Тэарэма 4: Няхай F – адвольнае поле, колца паліномаў F[x] ёсць колца галоўных ідэалаў.
Тэарэма 5: Колца рэштаў з 
– колца галоўных ідэалаў
Тэарэмы 4, 5 даказваюцца аналагічна тэарэме 3.
Азн.3: Ідэал I≠ K колца K наз.максімальным ідэалам колца K, калі ён не змяшчаецца ў большым ідэале колца K няроўным K, г.зн. 
Сцв.2: Ідэал (n) колца Z максімальны ў Z к.іт.к. n – просты лік.
Доказ: (0) - не максімальны ў Z, (1)=(-1) 
Z – не максімальны 
далей можна лічыць, што n> 0, бо n=(-n).
1. Няхай n – складовы лік, г.зн. n=KS, 1< k, s< n, тады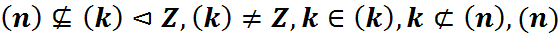 
не максімальны.
2. Няхай n - просты лік n=p, пакажам: (p) - максімальны ідэал Z. 
, з таго, што p – просты => p і a узаемна простыя і зн.адзінку можна запісаць: 1=pu+aδ, u, δ 
, p – максімальны ідэал Z. 
Сцв.3: Няхай F – поле, f(x) 
, ідэал (f(x)) максімальны ў F[x] к.іт.к. f(x) непрыводны паліном.