Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тэарэма 2 (2 крытэр падгрупы): к.іт.к. .
|
|
Азн.3: Няхай 
–групы з аперацыямі • і * адпаведна. Біекцыя адлюстравання 
наз. Ізамарфізмам G на 
, калі: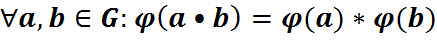 
.
Калі існуе які-небудзь ізамарфізм групы G на будзем казаць, што G ізаморфны ( 
).
Уласцівасці ізамарфізмаў групаў:
– ізамарфізм (адвольная група ізаморфная сама сабе) 
2. Калі 
– ізамарфізм, - ізамарфізм, тады 
– ізамарфізм; 
3. Калі , 
- ізамарфізмы групаў, тады 
– ізамарфізм (
).
15. A. Спараджальнае мноства (сістэма ўтваральных) падгрупы. Цыклічная група. Падгрупы цыклічнай групы.(8)
Сцв.1: Перасячэнне адвольнага мноства падгрупаў групы G ёсць падгрупа групы G.
Азн.1: Няхай M падмноства групы G, перасячэнне ўсіх падгрупаў групы G, якія змяшчаюць H. Будзем абазначаць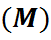 
і наз. падгрупай спароджаных M. Само M наз. спараджальным мноствам (ці мноствам утваральных) падгрупы (M). Відавочна (M) ёсць найменшая падгрупа групы G, якая змяшчае M, г.зн. калі 
.
Тэарэма 1: Няхай 
. Падгрупа спараджальная 
.
Азн.2: Група спароджаных аднаэлементавым мноствам элементаў наз. цыклічнай 
.
Вызначым ступені элемента a наступным чынам: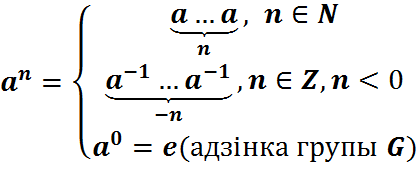 
. Паводле тэарэмы 1 цыклічная група спароджаныхт 
. Магчымы выпадкі:
1) 
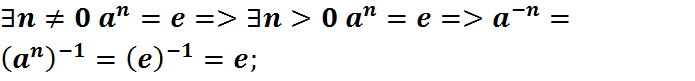
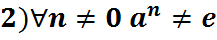
Азн.3: Парадкам 
наз. найменшы натуральны 
такі, што 
. Калі такога n няма, тады a наз. элементам бясконцага парадку. Абазначаецца 
.
Характарыстыка поля – парадак адзінкі ўдачыненні да складання.
Тэарэма 2: Няхай , 
, тады цыклічная група (a) – канцоўная група парадку n і 
. (*)
Тэарэма 3: Няхай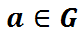 
|а|– бясконцага парадку, тады (a) – бясконцая і 
пры n≠ k.
заўвага*: |а|=n тады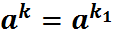 
. У прыватнасці 
.
Тэарэма 4: Адвольная падгрупа цыклічнай групы цыклічная.
Сцв.2: Няхай . Для адвольнага 
.
Сцв.3: У цыклічнай групе парадку n, для адвольнага натуральнага дзельніку k, ліку n (k|n) існуе адзіная падгрупа парадку k.
Тэарэма 5: 1) Адвольная бясконцая цыкічная група ізаморфная адытыўнай групе Z;
2) Адвольная канцоўная цыклічная група парадку n ізаморфная групе C(n) камплексных каранёў ступені n з адзінкі.
A. Сіметрычная група. Раскладанне падстановы ў здабытак незалежных цыклаў (без доказу). Парадак падстановы. Цотнасць падстановы (без доказу карэктнасці азначэння цотнасці). Зменназнакавая група.
Няхай 
. 
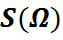– группа ў дачыненні да аперацыі множання адлюстраванняў. Элементы гэтай групы наз. падстановай мноства 
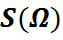. –сіметрычная група.
Калі канцоўнае множества прадку n зручна лічыць, 
– сіметрычная група ступені n.
Падстанову 
абазначым 
. З таго, што 
– падстанова, г.зн. біекцыя вынікае 
– перастаўленне лікаў 1, 2, …, n. Значыць лікі 1, 2, …, n сустракаюцца адзін і толькі aдзін раз. 
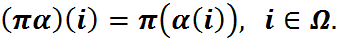
Тэарэма 1: Парадак групы 
роўны n! 
.
Азн.1: Няхай 
. Падстанова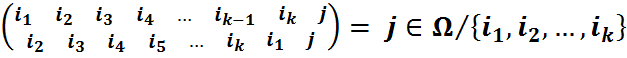 
абазначаецца ( 
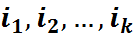) і наз. цыклам даўжыні k.
Азн.2: Цыклы ( 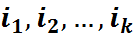) і ( 
) наз. незалежнымі ці неперасякальнымі, калі 
. Незалежныя цыклы перастановачныя.
Тэарэма 2: Адвольная падстанова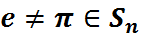 
ёсць здабытак незалежных цыклаў даўжынняў больш ці роўных за 2. Прычым расклад у здабытак незалежных цыклаў адназначны з дакладнасцю да парадку сумножніка.
Вынік 1: Парадак падстановы роўны НСК даўжыняў яе незалежных цыклаў.
Азн.3: Цыкл даўжыні 2 наз. транспазіцыяй
.
Вынік 2: Адвольная падстанова з раскладаецца ў здабытак транспазіцыяў.
Тэарэма 3: Няхай , 
– раскладанне у здабытак транспазіцыяў. Цотнасць ліку k не залежыць ад раскладу (1), а залежыць толькі ад .
Азн.4: Падстанова наз. цотнай, калі яна раскладацца ў здабытак цотнай колькасці транспазіцыяў, і няцотнай, калі яна раскладаецца ў здабытак няцотнай колькасці транспазіцыяў.
Вынік 2, спараджаецца мноствам ўсіх транс-цыяў.
Тэарэма 4: Мноства ўсіх цотных падстановаў з ёсць падгрупа групы парадку 
.
Група 
наз. зменназнакавай групай ступені n.
