
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
A. Алгебрычныя і трансцэндэнтныя элементы. Поле алгебрычных элементаў. Алгебрычная замкнёнасць поля алгебрычных лікаў (без доказаў).
|
|
Тэарэма1.  P алгебрычны над Р к.і.т.к [P(a): P]<.
P алгебрычны над Р к.і.т.к [P(a): P]<.
У гэтым выпадку [P(a): P] роўная ступені мінімальнага палінному элемента а над полем Р
Тэарэма2. Няхай F пашырэнне поля Р. А- мноства элементаў з F, алгебрычных над Р.Тады А-падполе поля F, A P
Азн1. Поле наз алгебрычна замкнёным, калі адвольны паліном ненулевой ступені над Р мае корань у поле Р
Тэарэма3. Поле алгебрычна лікаў алгебраічна замкнёнае.Гэта зн, што адвольнаы корань паліному ненулявой ступені, каэфіцыенты якога алгебрычныя лікі, ёсць алгебрычны лік.
Тэарэма4. Поле алгебрычных лікаў злічанае
Азн2. Элемент а  Р наз алгебрычным над Р, калі існуе ненулявы элемент
Р наз алгебрычным над Р, калі існуе ненулявы элемент  0
0  f(x)
f(x)  P[x] f(a)=0, трансцэндэнтным над Р, калі такого паліному няма
P[x] f(a)=0, трансцэндэнтным над Р, калі такого паліному няма
 0
0 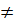 f(x)
f(x)  P[x] f(a)
P[x] f(a) 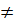 0
0
Прыклад.
21/2-алгебрычны лік
Е, П-трансцендентны лікі над Q
{Е, П-алгебрычны лікі над R}