A. Група. Азначэнне, прыклады, уласцівасці. Два крытэры падгрупы.

Азн.1: , на якім вызначаны бінарная алгебрычная аперацыя •, наз. групай, калі выконваюцца наступныя аксіёмы:

1. Аперацыя • асацыятыўная, г.зн.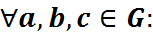

2. Існуе нейтральны элемент у дачыненні да аперацыі •, г.зн. такі элемент, што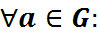

;

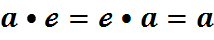існуе сіметрычны элемент, г.зн. такі элемент што .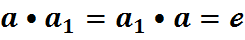

Прыклады: 1). Няхай F – поле, GL(n, F) - мноства ўсіх незвыродных матрыцаў ступені n над F. Тады на гэтым полі вызначана аперацыя множання det(a*b)=deta*detb≠ 0, калі a, b 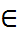GL(n, F). Аперацыя асацыятыўна, ёсць адзінкавая матрыца у гэтым полі, такая, што ,

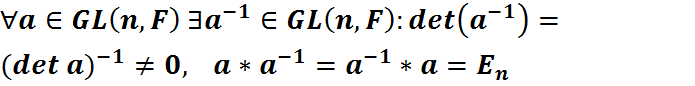
2). Няхай – мноства ўсіх біекцый 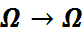. Падстановы . На 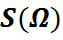вызначана аперацыя множання. Яна асацыятыўная, таму што множанне адвольных адлюстраванняў асацыятыўна, тоеснае адлюстраванне, такое, што 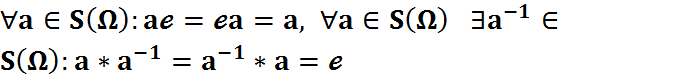Азн. 2: наз. падгрупай групы G, калі H –група ў дачыненні да аперацыяў, вызначаных ў G. Абазначаецца H< G.

Тэарэма 1 (1 крытэр падгрупы): к.іт.к: 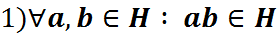.