Односторонние пределы.

Определение. Число А называется правым пределом функции f(x) при х→ х₀, если для любого сколь угодно малого числа e> 0 можно указать такое число δ > 0 (зависящее от e, δ =δ (e)), что для всех хÎ Х таких, что х₀< х< х₀+δ выполняется неравенство |f(х)-A|< e. (при попадании точки х в правую полуокрестность точки х₀).

e> 0 δ =δ (e) x: х₀< х< х₀+δ |f(х)-A|< e (1)

f(х₀+0)= = = А₊ или f(x₀+0)=A

Определение. Число А называется левым пределом функции f(x) при х→ х₀, если для любого сколь угодно малого числа e> 0 можно указать такое число δ =δ (e), что для всех хÎ Х таких, что х₀-d< х< х₀ выполняется неравенство |f(х)-A|< e.

(при попадании точки х в левую полуокрестность точки х₀).

e> 0 δ =δ (e) x: х₀-δ < х< х₀ |f(х)-A|< e (2)

f(a-0)= =А_-. или f(x₀-0)=A

Утверждения. 1) Если у функции f(x) при при х→ х₀ существует предел А в обычном смысле (т.е. двусторонний), то существуют оба односторонних предела f(х₀+0) и f(х₀+0) и они оба равны А.

2) Если у функции f(x) при при х→ х₀ существуют оба односторонних предела f(х₀+0) и f(х₀+0) и они оба равны А, то у f(x) при при х→ х₀ существует двусторонний предел, равный числу А.

Пример. (График).

Расширение понятия предела функции (Понятие предела функции на бесконечности. Бесконечные пределы.) (пример на каждый случай)

Определение 1. Число А называется пределом функции f(x) при х→ +∞, если для любого сколь угодно малого числа e> 0 найдется такое число Т (зависящее от e, Т=Т(e)), что для всех х таких, что x> Т выполняется неравенство |f(х)-A|< e.

Т.е. e> 0 Т=Т(E) x: x> Т |f(х)-A|< E (1) =А

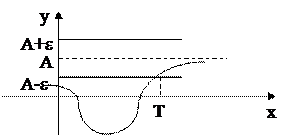
Определение 2. Число А называется пределом функции f(x) при х→ -∞, если для любого сколь угодно малого числа e> 0 найдется такое число Т (зависящее от e, Т=Т(e)), что для всех х таких, что x< Т выполняется неравенство |f(х)-A|< e.

Т.е. e> 0 Т=Т(E) x: x< Т |f(х)-A|< E (2) =А

Определение 3. Пределом функции f(x) при х→ х₀ является +¥, если для любого сколь угодно большого числа С> 0 найдется такое число d=d(С), что для всех х таких, что 0< |x-x₀|< δ выполняется неравенство f(х)> C.

Т.е. C> 0 d=d(С ) x: 0< |x-x₀|< δ Þ f(х)> C (3) =+¥

Определение 4. Пределом функции f(x) при х→ х₀ является -¥, если для любого числа С< 0 найдется такое число d=d(С), что для всех х таких, что 0< |x-x₀|< δ выполняется неравенство f(х)< C.

Т.е. C< 0 d=d(С ) x: 0< |x-x₀|< δ Þ f(х)< C (4) =-¥

Пример. f(x)= 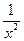- график.

Определение 5. Пределом функции f(x) при х→ +¥ является +¥, если для любого сколь угодно большого числа С> 0 найдется такое число T=T(С), что для всех х таких, что x> T выполняется неравенство f(х)> C.

Т.е. C> 0 T=T(С ) x: x> T Þ f(х)> C (5) =+¥

Определение 6. Пределом функции f(x) при х→ +¥ является -¥, если для любого числа С< 0 найдется такое число T=T(С), что для всех х таких, что x> T выполняется неравенство f(х)< C.

Т.е. C< 0 T=T(С ) x: x> T Þ f(х)< C (6) =-¥

Определение 7. Пределом функции f(x) при х→ -¥ является +¥, если для любого сколь угодно большого числа С> 0 найдется такое число T=T(С), что для всех х таких, что x< T выполняется неравенство f(х)> C.

Т.е. C> 0 T=T(С ) x: x< T Þ f(х)> C (7) =+¥

Определение 8. Пределом функции f(x) при х→ -¥ является -¥, если для любого числа С< 0 найдется такое число T=T(С), что для всех х таких, что x< T выполняется неравенство f(х)< C.

Т.е. C< 0 T=T(С ) x: x< T Þ f(х)< C (8) =-¥