
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства б/б величин.
|
|
1. Если одна из трех функций f(x), -f(x), ç f(x)ç является б.б. при х→ х0, то и две другие функции также являются б.б. при х→ х0.
2. Произведение б/б функции на функцию, предел которой отличен от нуля, есть б/б величина.
3. Сумма б/б величины и ограниченной функции есть б/б величина.
4. Частное от деления б/б функции на функцию, имеющую предел, есть б/б функция.
Например, функция f(x)= 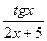 - является частным от деления б/б функции tg x при х→ П/2 на функцию 2х+5 имеющую предел П+5 при х→ П/2.
- является частным от деления б/б функции tg x при х→ П/2 на функцию 2х+5 имеющую предел П+5 при х→ П/2.
Доказательство св-ва 2. (остальные – аналогично).
Пусть f(x) – б.б. функция при х→ х0, т.е. 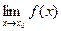 =∞ и
=∞ и  =с (с≠ 0).
=с (с≠ 0).
Докажем, что f(x)× j(х) - б.б. функция при х→ х0.
Рассмотрим последовательность хn→ x0, n→ ¥ (предполагается, что xn берутся из окрестности x0 и xn≠ x0)
По условию  =с (с≠ 0). Но тогда и
=с (с≠ 0). Но тогда и 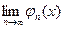 =с (с≠ 0).
=с (с≠ 0).
По условию f(x) – б.б. функция при х→ х0, но тогда и f(xn) – б.б. функция при n→ ¥. Следовательно, f(xn)× j(хn) - б.б. последовательность, как произведение б.б. последовательности и последовательности, имеющей конечный, отличный от 0 предел.
Т.к. последовательность хn – любая сходящаяся к х0, то заключаем, что
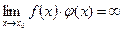
Это означает, что функция f(x)× j(х) - б.б. функция при х→ х0. ч.т.д.