Сравнение бесконечно малых величин.

Пусть при х→ х₀ функции α (х) и β (х) являются б.м., и пусть β (х)≠ 0 тогда

1. если 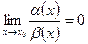, то α (х) называется б.м. более высокого порядка, чем β (х) (α (х) имеет более высокий порядок малости, чем β (х) при х→ х₀)

Пишут a(х)=о(b(х)) при х→ х₀ (о малое)

Пример. Покажем, что при х→ 0 функция х^k (k> 1) – б.м. более высокого порядка, чем х. Действительно, 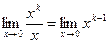=0, т.к. по условию k> 1.

2. если =А≠ 0, то α (х) и β (х) называются б.м. одного порядка (имеют одинаковую «скорость» стремления к 0).

Пример. Покажем, что при х→ 0 функции sin kx и mx (k≠ 0, m≠ 0)- б.м. одного порядка. Действительно,

3. если =1, то α (х) и β (х) называются эквивалентными б.м.: α (х)~β (х).

Пример. Покажем, что при х→ 0 функции sin x и tg x (k≠ 0, m≠ 0)- б.м. одного порядка. Действительно,

4. если =¥, то функцию α (х) называют б.м. более низкого порядка по сравнению с β (х) при х→ х₀.

5. если отношение не имеет придела при х→ х₀, то говорят, что б.м. функции α (х) и β (х) не сравнимы при х→ х₀.

Пример. Функции a(х)= 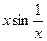и b(х)=х – б.м. при х→ 0. Имеем 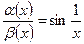, но не имеет предела при х→ 0. Значит, α (х) и β (х) не сравнимы при х→ 0.

6. если =А≠ 0, то α (х) называется б.м. n –го порядка относительно β (х) при х→ х₀. (n> 0, не обязательно целое).

Из предыдущих пунктов следует, что

1) Если n=1, то функция α (х) б.м. одного порядка с β (х) при х→ х₀.

2) Если n> 1, то функция α (х) б.м. более высокого порядка по сравнению с β (х) при х→ х₀.

3) Если n< 1, то функция α (х) б.м. более низкого порядка по сравнению с β (х) при х→ х₀.

Теорема 1. Произведение двух б.м. величин является б.м. величиной более высокого порядка по сравнению с каждым из сомножителей.

Доказательство. Пусть при х→ х₀ функции α (х) и β (х) являются б.м., γ (х)=α (х)× β (х). Докажем, что γ (х)=о(α (х)) и γ (х)=о(β (х)) при х→ х₀. Имеем

, а это означает, что γ (х)=о(α (х)) при х→ х₀.

Аналогично, , а это означает, что γ (х)=о(β (х)) при х→ х₀. ч.т.д.

Теорема 2. Разность двух эквивалентных бесконечно малых функций является бесконечно малой функцией по сравнению с каждой из них.

Доказательство. Пусть при х→ х₀ функции α (х) и β (х) являются б.м., и α (х)~β (х). Положим γ (х)=α (х)-× β (х). Докажем, что γ (х)=о(α (х)) и γ (х)=о(β (х)) при х→ х₀. Имеем

, По условию, т.к. α (х)~β (х), то =1. Следовательно, =1-1=0. Значит, γ (х)=о(α (х)) при х→ х₀.

Аналогично, 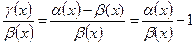, По условию, т.к. α (х)~β (х), то =1. Следовательно, =1-1=0. Значит, γ (х)=о(β (х)) при х→ х₀. ч.т.д.