Первый замечательный предел.

= 1 (1)

Доказательство. Т.к. , то = , если эти пределы существуют. Поэтому достаточно установить и показать, что равен 1 хотя бы один односторонний предел. Покажем, что = 1 (2). Поэтомуможно рассматривать лишь значения х: 0< x< .

Рассмотрим круг с центром в точке О и радиусом R 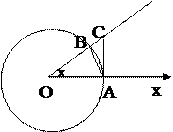. Пусть ОВ подвижный радиус, образующий с осью Ох угол х (0< x< ).

Площадь ∆ АОВ меньше площади сектора АОВ, которая меньше площади прямоугольного ∆ АОС.

S_{∆ AOB}< S_{сек. АОВ}< S_{∆ AOC}

S_{∆ AOB}= ОА∙ ОВ∙ sin x= R∙ R∙ sin x= R²∙ sin x

S_{сек. АОВ}= R²∙ x, (площадь кругового сектора, ограниченного дугой с градусной мерой a: S= )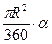

S_{∆ AOC}= AO∙ OC= AO∙ AС∙ tg x= R²∙ tg x.

Получаем R²∙ sin x< R²∙ x< R²∙ tg x

Делим полученное неравенство на R², получаем:

sin x< x< tg x (хÎ ) (3)

Делим полученное неравенство на sin x (sin x> 0), получаем:

1< < или cos x< < 1

Вычитая из 1 каждый из членов последнего неравенства, получим

0< 1- < 1-cos x (4)

Но 1-cos x=2sin² < 2sin < x (в силу (3))

Следовательно, вместо неравенства (4) будем иметь: 0< 1- < х (5)

Возьмем e> 0 любое, сколь угодно малое (можно считать, что e< ). Если положить d=e (d> 0), то " х, удовлетворяющих неравенству 0< x< d, будет

0< 1- < e

Т.к. если x< d, то x< e. Значит, < eÛ < e, если 0< x< d.

Последнее означает, что 1= . Соотношение (2) установлено, а значит доказано и (1) ч.т.д.

(Эти неравенства верны и при – < x< 0, т.к. функции cos²x и четные).

Покажем, что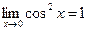

cos²x=1-sin²x. Покажем, что 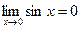при 0< ç xç < < 1, тогда

< 1Þ ç sin xç < ç xç

Возьмем e> 0, d=e. 0< ç xç < dÞ ç sin xç < ç xç < d=e. Т.е.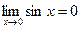

Тогда =1-0=1

Переходим к пределу при х→ 0: cos²x→ 1, 1→ 1 при х→ 0.

Следовательно, по теореме о пределе промежуточной функции, получим = 1. Ч.т.д.

Пример. = 2 (заменой (т.е. через сложную функцию) и без).