Бесконечно малые функции (величины) и их свойства.

Определение. Функция α (х) называется бесконечно малой (б/м) функцией при х → х₀, или при х → ∞, если: α (х)=0. х₀ может быть как число, так и -¥, +¥, ¥.

Т.е. ε > 0 δ =δ (ε)> 0 х: 0< |х–х₀|< δ |α (х)|< ε

Аналогично можно сформулировать определение бесконечно малой при х → ∞

ε > 0 S=S(ε)> 0 х: |х| > S |α (x)|< ε

Например, y=cos x - б/м при х→ П/2, у= б/м при х→ ∞.

Связь бесконечно малых величин с пределами функций.

Теорема. Функция f(x) имеет при х→ х₀ (х → ∞) предел, равный А, тогда и только тогда, когда ее можно представить как сумму числа A и бесконечно малой функции α (х) при х → х₀ (х → ∞).

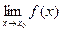=А 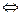f(x)-A=α (x)

Доказательство.Необходимость. Докажем теорему для любого случая х→ х₀. По условию f(x) = A. Это означает, что для любого ε > 0 существует такое число δ > 0, что для всех х≠ х₀ и удовлетворяющих условию |х–х₀|< δ будет верно неравенство |f(x)–A|< ε, или, обозначив α (х)=f(x)–A, справедливо неравенство |α (х)|< ε. Это и означает, что α (х) есть бесконечно малая при х→ х₀. ■

Достаточность. □ По условию α (х)=f(x)–A есть бесконечно малая при х→ х₀, то для любого числа ε > 0 существует такое число δ > 0, что при всех х≠ х₀ и удовлетворяющих условию |х–х₀|< δ верно неравенство |α (х)|=|f(x)–A|< ε.

Это и означает, что f (x)= A. ■

Доказательство через последовательности. Необходимость. Возьмем последовательность х₁, x₂, …, x_n, … значений х любую, но такую, что x_nÎ и x_n®x₀ при n®¥.

По условию 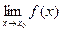= А. Тогда f(x_n)®A при (f(x_n)-A)=α (х_n)®0 при n®¥.

Т.к. последовательность х₁, x₂, …, x_n, …-любая, сходящаяся к х₀, то = 0Û

Û = 0. А последнее и означает, что разность f(x)–A – б.м. при х®х₀.

Достаточность. Возьмем последовательность х₁, x₂, …, x_n, … значений х любую, но такую, что x_nÎ и x_n®x₀ при n®¥.

По условию a(х)=f(x)–A – б.м. при х®х₀, т.е. = =0. Но тогда

α (х_n)®0 при n®¥ Û (f(x_n)-A)®0 при n®¥.

Т.к. последовательность х₁, x₂, …, x_n, …-любая, сходящаяся к х₀, то f (x)= A.

Свойства бесконечно малых величин:

1. Если одна из трех функций f(x), -f(x), ç f(x)ç является б.м. при х→ х₀, то и две другие функции также являются б.м. при х→ х₀.

2. Алгебраическая сумма конечного числа б/м величин есть величина б/м.

3. Произведение б/м величины на ограниченную функцию (в том числе на постоянную, на другую б/м) есть величина б/м.

4. Частное от деления б/м величины на функцию, предел которой отличен от нуля, есть величина б/м.

Доказательство через последовательности или через определение предела функции при А=0.

Пример. Доказать, что функция f(x)=(х-1)sin является бесконечно малой при х→ 1.

Т.к. =0, т.е. (х-1) – б.м. при х→ 1, а функция sin ограничена (т.к. ), то функция f(x) является произведением б.м. функции на ограниченную. Следовательно, функция f(x)=(х-1)sin является бесконечно малой при х→ 1.