Пределы монотонных функций.

Теорема 1. (б.д.?)Пусть функция f(x) монотонно возрастает (строго возрастает) на множестве Х. Пусть в любой левой полуокрестности точки х₀ (х₀-d; х₀) существуют точки множества Х, отличные от х₀. (Число х₀ может быть как конечным, так и равным +¥, в этом случае левая полуокрестность это хÎ Х: x< x₀).

1) Если при этом функция f(x) ограничена сверху, т.е. существует число С такое, что f(x)£ С хÎ Х, то при х→ х₀-0 функция f(x) имеет конечный предел.

2) Если f(x) сверху не ограничена, то .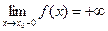

Доказательство.

1) Т.к. функция f(x) ограничена сверху, тогда существует точная верхняя граница множества {f(x)}, xÎ X. Пусть m= . Тогда хÎ Х f(x)£ m. (1)

Возьмем сколь угодно малое e> 0 и рассмотрим число m-e.

Т.к. m-e< m, то по свойству супремума на множестве {f(x)}, xÎ X, обязательно найдется элемент > m-e.

Т.к. функция f(x) монотонно возрастает на множестве Х, то хÎ Х, удовлетворяющих условию х> будет f(x)³ и, следовательно, f(x)> m-e (2).

Т.о. хÎ Х: х> будут выполняться оба неравенства (1) и (2), т.е.

m-e< f(x)£ m, значит, m-e< f(x)£ m+e Û ç f(x)-mç < e.

а) Положим d=а- или =а-d, где а – конечное число. В этом случае хÎ Х, удовлетворяющих неравенству а-d< x< a, будет ç f(x)-mç < e, а это означает m=

б) Положим D= , если а=+¥ (можно считать, что =D> 0). В этом случае хÎ Х, удовлетворяющих неравенству x> D, будет ç f(x)-mç < e, а это означает m=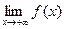

2) (б.д.?) Допустим, что функция f(x) не ограничена сверху, т.е. не ограничено сверху множество {f(x)}, xÎ X. Это значит, что какое бы большое число М> 0 ни взять на множестве {f(x)}, xÎ X, обязательно найдется хотя бы один элемент такой, что будет > М.

Т.к. функция f(x) монотонно возрастает на множестве Х, то хÎ Х, удовлетворяющих условию х> будет f(x)³ и, следовательно, f(x)> М.

а) Положим d=а- или =а-d, где а – конечное число. В этом случае хÎ Х, удовлетворяющих неравенству а-d< x< a, будет f(x)> М, а это означает =+¥.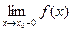

б) Положим D= , если а=+¥ (можно считать, что =D> 0). В этом случае хÎ Х, удовлетворяющих неравенству x> D, будет f(x)> М, а это означает 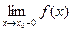=+¥. Ч.т.д.

Теорема 2. Пусть функция f(x) монотонно убывает (строго убывает) на множестве Х. Пусть в любой левой полуокрестности точки х₀ (х₀-d; х₀) существуют точки множества Х, отличные от х₀. (Число х₀ может быть как конечным, так и равным +¥, в этом случае левая полуокрестность это хÎ Х: x< x₀).

1) Если при этом функция f(x) ограничена снизу, т.е. существует число М, такое, что f(x)³ М хÎ Х, то при х→ х₀-0 функция f(x) имеет конечный предел.

2) Если f(x) снизу не ограничена, то .

Общий признак существования конечного предела. (Критерий Коши)

Теорема (Критерий Коши). Для того, чтобы существовал предел (конечный) функции f(x) при х→ х₀ (х₀ может быть либо конечной точкой, либо ±¥), необходимо и достаточно, чтобы функция была определена в окрестности точки х₀ (за исключением, быть может, самой точки х₀), и для любого сколь угодно малого e> 0 существовала такая окрестность V(x₀) точки х₀, что каковы бы ни были точки х₁, х₂Î V(x₀), х₁, х₂≠ х₀ выполняется неравенство |f(х₁)-f(х₂)|< e, т.е.

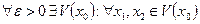Þ |f(х₁)-f(х₂)|< e.

Замечание. В случае, когда х₀=+¥ под условием понимается, что найдется такое число D=D(e), что х₁> D, x₂> D.

В случае, когда х₀=-¥ под условием понимается, что найдется такое число D=D(e), что х₁< D, x₂< D.